The force between two poles is reduced to P newton, when their original separation is increased to x times, it is increased to Q newton, when their separation is made 1/xth of their original value. Then the relation between P and Q is
Q = XP
Q=X^2P
Q=X^3P
Q=X^4P
To solve the problem, we need to establish the relationship between the forces P and Q based on the changes in separation distance between the two poles.
1. Understanding the Force Equation:
The force F between two poles (or masses) is given by the formula:
F=k⋅m1⋅m2r2
where k is a constant, m1 and m2 are the masses of the two poles, and r is the distance between them.
2. Case 1 - Increased Separation:
When the separation is increased to x times the original distance, the force becomes P. Thus, we can write:
P=k⋅m1⋅m2(x⋅r)2
Simplifying this gives:
P=k⋅m1⋅m2x2⋅r2
Rearranging, we find:
k⋅m1⋅m2=P⋅x2⋅r2(Equation 1)
3. Case 2 - Decreased Separation:
When the separation is made 1x times the original distance, the force becomes Q. Thus, we can write:
Q=k⋅m1⋅m2(1x⋅r)2
Simplifying this gives:
Q=k⋅m1⋅m21x2⋅r2=k⋅m1⋅m2⋅x2⋅1r2
Rearranging, we find:
k⋅m1⋅m2=Q⋅r2x2(Equation 2)
4. Equating the Two Equations:
From Equation 1 and Equation 2, we have:
P⋅x2⋅r2=Q⋅r2x2
Since r2 is common in both sides, we can cancel it out (assuming r≠0):
P⋅x2=Q⋅1x2
5. Final Relation:
Rearranging gives us:
P⋅x4=Q
Thus, the relationship between P and Q is:
Q=P⋅x4
Conclusion:
The relation between P and Q is:
Q=P⋅x4
The force F between two poles (or masses) is given by the formula:
F=k⋅m1⋅m2r2
where k is a constant, m1 and m2 are the masses of the two poles, and r is the distance between them.
When the separation is increased to x times the original distance, the force becomes P. Thus, we can write:
P=k⋅m1⋅m2(x⋅r)2
Simplifying this gives:
P=k⋅m1⋅m2x2⋅r2
Rearranging, we find:
k⋅m1⋅m2=P⋅x2⋅r2(Equation 1)
When the separation is made 1x times the original distance, the force becomes Q. Thus, we can write:
Q=k⋅m1⋅m2(1x⋅r)2
Simplifying this gives:
Q=k⋅m1⋅m21x2⋅r2=k⋅m1⋅m2⋅x2⋅1r2
Rearranging, we find:
k⋅m1⋅m2=Q⋅r2x2(Equation 2)
From Equation 1 and Equation 2, we have:
P⋅x2⋅r2=Q⋅r2x2
Since r2 is common in both sides, we can cancel it out (assuming r≠0):
P⋅x2=Q⋅1x2
Rearranging gives us:
P⋅x4=Q
Thus, the relationship between P and Q is:
Q=P⋅x4
The relation between P and Q is:
Q=P⋅x4
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
Explore 95 Videos
- ALTERNATING CURRENTBook:AAKASH SERIESChapter:ALTERNATING CURRENTExercise:EXERCISE - III
Explore 24 Videos
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:LAW OF MOTION
Explore 128 Videos
Similar Questions
IF the different between the roots of x2−px+q=0 is 2, then the relation between p , and q is
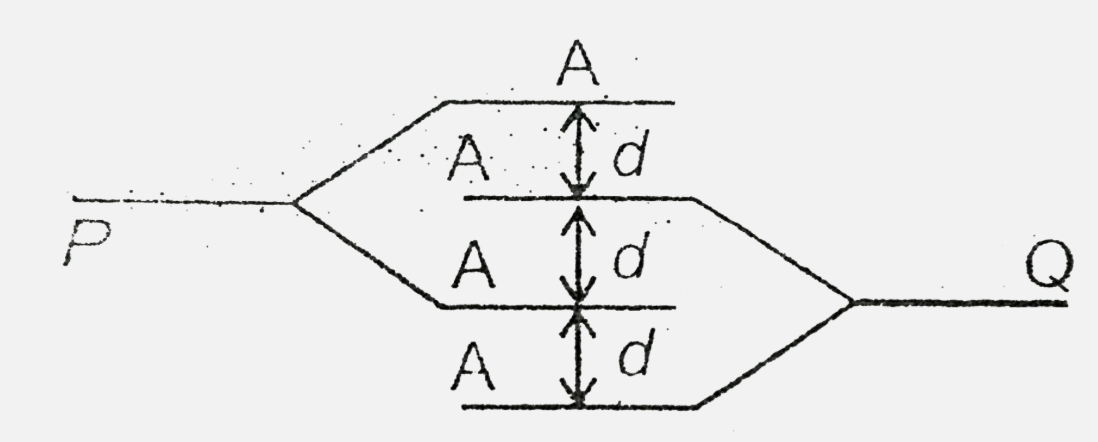
View SolutionIf the area of each plate is A and the separation between them is d, then find the equivalent capacitance between P and Q
View SolutionThe focal length of a combination of two lenses is doubled if the separation between them is doubled. If the separation is increased to 4 times, the magnitude of focal length is
View SolutionWhen the operating voltage in an -X-ray tube is increased to 3 times the original value, the shortest wavelength shifts by 25 nm. Find the original value of the operating voltage.
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the temperature is raised through 1∘C the volume is increased by 1273 th times of the original volume . This is
View SolutionWhen the separation between two charges is increase the electric potential energy of the charges.
View SolutionIn a parallel plate capacitor, the separation between the plates is 3mm with air between them. Now a 1mm thick layer of a material of dielectric constant 2 is introduced between the plates due to which the capacity increases. In order to bring its capacity of the original value, the separation between the plates must be made- 1.)1.5 mm 2.)2.5 mm 3.)3.5 mm 4.)4.5 mm
View SolutionForce between two identical bar magnets whose centres are r metre apart is 4.8N, when their axes are in the same line. If separation is increased to 2r, the force between them is reduced to
View Solution

