For the same angle of incidence, the angles of refraction in three different media A, B and Care 30∘,60∘and45∘ respectively. In which medium will the velocity or light be maximum?
To solve the problem of determining in which medium the velocity of light is maximum given the angles of refraction in three different media, we can follow these steps:
Step 1: Understand the relationship between the angles of incidence and refraction
According to Snell's law, the relationship between the angles of incidence (i) and refraction (r) in two different media is given by:
n1sin(i)=n2sin(r)
Where n1 and n2 are the refractive indices of the respective media.
Step 2: Identify the angles of refraction
From the problem, we have the angles of refraction for the three media:
- Medium A: rA=30∘
- Medium B: rB=60∘
- Medium C: rC=45∘
Step 3: Relate the speed of light in different media to the angles of refraction
The speed of light in a medium is inversely proportional to its refractive index:
v=cn
Where c is the speed of light in vacuum. The refractive index can also be expressed in terms of the angles of refraction:
n=sin(i)sin(r)
Thus, we can express the speed of light in each medium as:
v∝sin(r)
Since the angle of incidence i is constant for all three media.
Step 4: Calculate the sine of the angles of refraction
Now we calculate the sine values for each angle of refraction:
- For Medium A:
sin(30∘)=12
- For Medium B:
sin(60∘)=√32
- For Medium C:
sin(45∘)=√22
Step 5: Compare the values
We can now compare the proportional speeds of light in each medium based on the sine values:
- Medium A: vA∝sin(30∘)=12
- Medium B: vB∝sin(60∘)=√32
- Medium C: vC∝sin(45∘)=√22
Step 6: Determine which medium has the maximum speed
To determine which medium has the maximum speed, we compare the values:
- 12 (Medium A)
- √32 (Medium B)
- √22 (Medium C)
Since √3≈1.732 and √2≈1.414, we find:
- √32 is greater than both 12 and √22.
Conclusion
Thus, the velocity of light is maximum in Medium B.
According to Snell's law, the relationship between the angles of incidence (i) and refraction (r) in two different media is given by:
n1sin(i)=n2sin(r)
Where n1 and n2 are the refractive indices of the respective media.
From the problem, we have the angles of refraction for the three media:
- Medium A: rA=30∘
- Medium B: rB=60∘
- Medium C: rC=45∘
The speed of light in a medium is inversely proportional to its refractive index:
v=cn
Where c is the speed of light in vacuum. The refractive index can also be expressed in terms of the angles of refraction:
n=sin(i)sin(r)
Thus, we can express the speed of light in each medium as:
v∝sin(r)
Since the angle of incidence i is constant for all three media.
Now we calculate the sine values for each angle of refraction:
- For Medium A:
sin(30∘)=12
- For Medium B:
sin(60∘)=√32
- For Medium C:
sin(45∘)=√22
We can now compare the proportional speeds of light in each medium based on the sine values:
- Medium A: vA∝sin(30∘)=12
- Medium B: vB∝sin(60∘)=√32
- Medium C: vC∝sin(45∘)=√22
To determine which medium has the maximum speed, we compare the values:
- 12 (Medium A)
- √32 (Medium B)
- √22 (Medium C)
- √32 is greater than both 12 and √22.
Thus, the velocity of light is maximum in Medium B.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)57videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS )24videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III3videos
SEMICONDUCTOR DEVICES
Similar Questions
For the same angle of incidence, the angles of refraction in three different media A, B and C are15∘,25∘ and 35∘ respectively. In which medium, will the velocity of light be minimum ?
View SolutionFor the same angle of incidence in media P,Q and R, the angles of refraction are 35∘,25∘,15∘ respectively. In which medium will the velocity of light be minimum?
View SolutionWrite a relationship between angle of incidence and angle of refraction for a given pair of media.
View SolutionLooking at the angle of refraction in the figures given Fig. B, which medium will have the maximum value of refractive index and in which medium will the speed of light be the least?
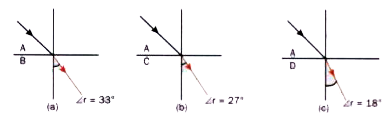 View Solution
View SolutionThe velocities of light in two different media are 2*108m/s and 2.5 * 108m/s respectively.The critical angle for these media is
View SolutionA ray of light is incident on the surface of seperation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the velocity of light in the medium?
View SolutionIn the diagrams given in Figure C, draw the angle of incidence and the angle of refraction. Identify which medium is rarer and which medium is denser.
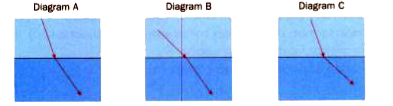 View Solution
View SolutionIf a ray of light in a denser medium strikes a rarer medium at an angle of incidence i, the angles of reflection and refraction are respectively, r and r' If the reflected and refraction rays are at right angles to each other, the critical angle for the given pair of media is
View SolutionHow are the angle of incidence and angle of refraction related to each other when :
(a) a ray of light travels from rare to dense medium,
(b) a ray of light travles from dense to rare medium ?View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
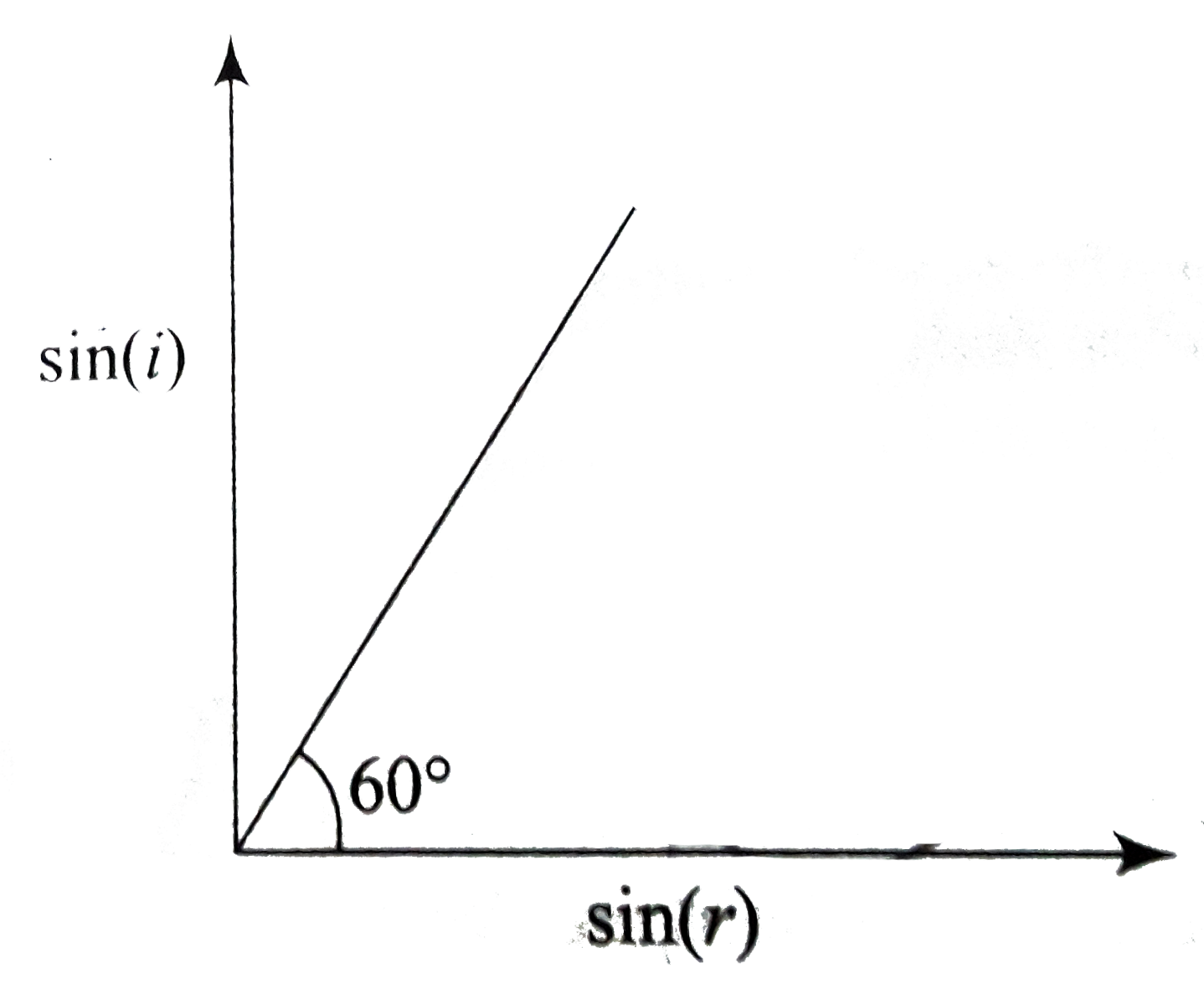 View Solution
View Solution

