If θcin the critical angle, write the deviation value when the ray travels from denser to rarer for i>θc.
Step by step video & image solution for If theta _c in the critical angle, write the deviation value when the ray travels from denser to rarer for i gt theta_c. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)57videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS )24videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III3videos
SEMICONDUCTOR DEVICES
Similar Questions
When a wave travels from a denser to rarer medium, then
View SolutionWhen a light ray enters from a denser medium to a rarer medium.
View SolutionState whether the following statement is true or false ? If the angle of incidence is greater than the critical angle, light is not refracted at all, when it falls on the surface from a denser medium to a rarer medium.
View SolutionLet the refractive index of a denser medium with respect to a rarer medium be n12 and its critical angle be θc. At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is 90∘, Angle A given by -
View SolutionLet the refractive index of a denser medium with respect to a rarer medium be n12 and its critical angle be θc. At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is 90∘, Angle A given by -
View SolutionFind the angle θa made by the light ray when it gets refracted from water to air, as shown in Fig .
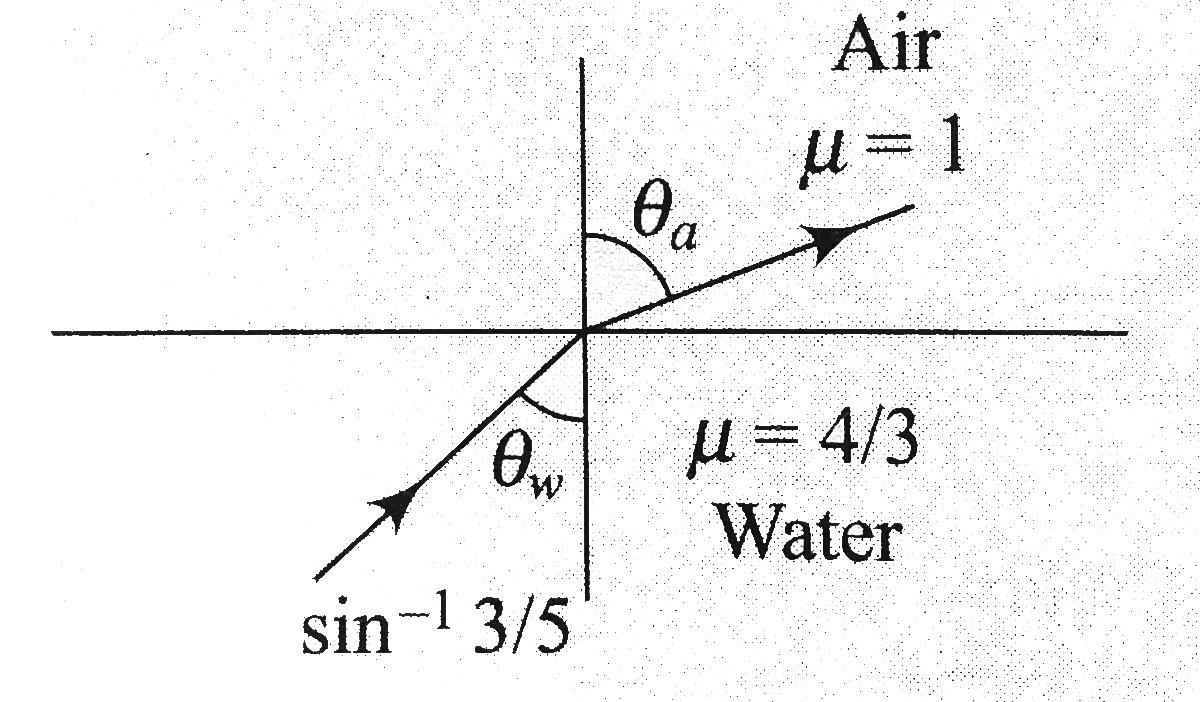 View Solution
View Solution(I) How does the refractive index of a medium depends on the wavelength of light used?
(II)Which is greater, angle of incidence or angle of refraction, when light travels from denser medium to rarer medium.View SolutionFill the blanks to complete the following sentence:
Q: When light travels from a denser to a rarer medium, its speed ______View SolutionSTATEMENT -1 : The critical angle is defined when light goes from denser medium to the rarer medium.
and
STATEMENT - 2 : In total internal reflection, intensity of light remains same.View SolutionStatement I: A ray is incident from outside on a glass sphere surrounded by air as shown in Figure. This ray may suffer total internal reflection at the second interface.

Statement II: For a ray going from a denser to rarer medium, the ray may suffer total internal reflection.View Solution


