For the same angle of incidence in media P,Q and R, the angles of refraction are 35∘,25∘,15∘ respectively. In which medium will the velocity of light be minimum?
To determine in which medium the velocity of light is minimum, we can use Snell's Law and the relationship between refractive index and the speed of light in different media.
1. Understanding the Problem: We have three media (P, Q, and R) with the same angle of incidence, and the angles of refraction are given as:
- Medium P: rP=35∘
- Medium Q: rQ=25∘
- Medium R: rR=15∘
2. Applying Snell's Law: Snell's Law states that:
n=sin(i)sin(r)
where n is the refractive index, i is the angle of incidence, and r is the angle of refraction.
3. Refractive Index and Angle of Refraction: Since the angle of incidence is the same for all three media, we can say:
nP∝1sin(35∘),nQ∝1sin(25∘),nR∝1sin(15∘)
This implies that the refractive index is inversely proportional to the sine of the angle of refraction.
4. Comparing Sine Values: We know that:
- sin(35∘)>sin(25∘)>sin(15∘)
Thus:
- nP<nQ<nR
This means medium P has the lowest refractive index and medium R has the highest refractive index.
5. Relating Refractive Index to Velocity: The refractive index is also related to the speed of light in a medium:
n=cv
where c is the speed of light in vacuum and v is the speed of light in the medium. Therefore, a higher refractive index means a lower speed of light in that medium.
6. Conclusion: Since medium R has the highest refractive index, it will have the lowest speed of light. Thus, the velocity of light will be minimum in medium R.
Final Answer:
The velocity of light will be minimum in medium R.
- Medium P: rP=35∘
- Medium Q: rQ=25∘
- Medium R: rR=15∘
n=sin(i)sin(r)
where n is the refractive index, i is the angle of incidence, and r is the angle of refraction.
nP∝1sin(35∘),nQ∝1sin(25∘),nR∝1sin(15∘)
This implies that the refractive index is inversely proportional to the sine of the angle of refraction.
- sin(35∘)>sin(25∘)>sin(15∘)
Thus:
- nP<nQ<nR
This means medium P has the lowest refractive index and medium R has the highest refractive index.
n=cv
where c is the speed of light in vacuum and v is the speed of light in the medium. Therefore, a higher refractive index means a lower speed of light in that medium.
The velocity of light will be minimum in medium R.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET - II]
6 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET - III]
9 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]
3 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
For the same angle of incidence, the angles of refraction in three different media A, B and C are15∘,25∘ and 35∘ respectively. In which medium, will the velocity of light be minimum ?
View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
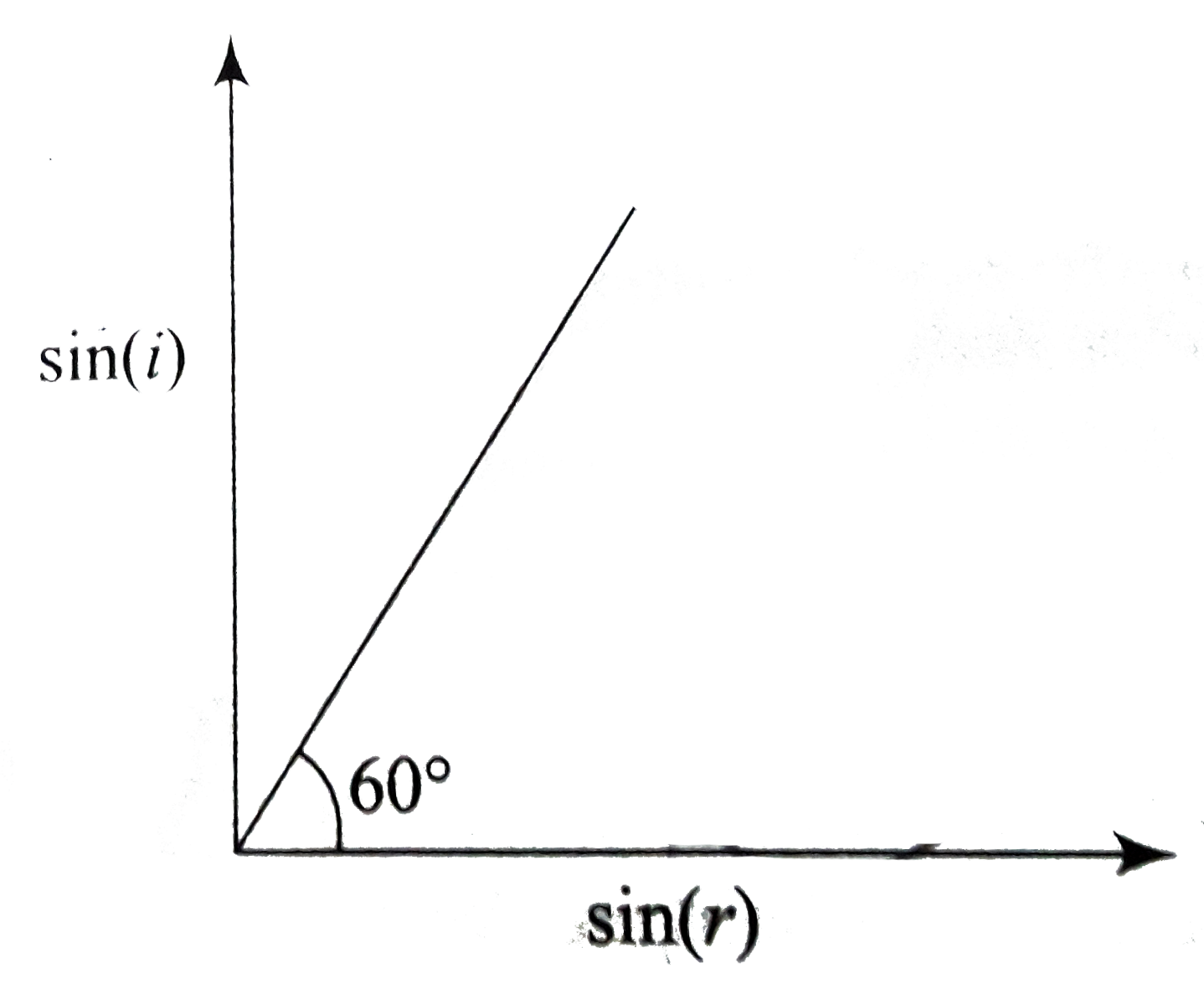
View SolutionWrite a relationship between angle of incidence and angle of refraction for a given pair of media.
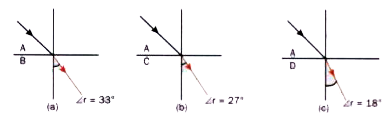
View SolutionLooking at the angle of refraction in the figures given Fig. B, which medium will have the maximum value of refractive index and in which medium will the speed of light be the least?
View SolutionIf a ray of light in a denser medium strikes a rarer medium at an angle of incidence i, the angles of reflection and refraction are respectively, r and r' If the reflected and refraction rays are at right angles to each other, the critical angle for the given pair of media is
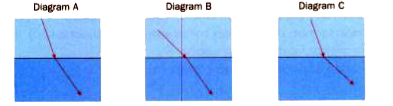
View SolutionIn the diagrams given in Figure C, draw the angle of incidence and the angle of refraction. Identify which medium is rarer and which medium is denser.
View SolutionA ray of light is incident at an angle i from denser to rare medium. The reflected and the refracted rays are mutually perpendicular. The angle of reflection and the angle of refraction are respectively r and r'. Then the critical angle will be:
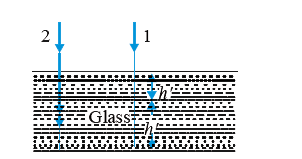
View SolutionA ray of monochromatic light is incident on the plane surface of separation between two media x and y with angle of incidence i in the medium x and angle of refraction r in the medium y. The graph shows the relation between sin i and sin r.

View SolutionA ray of light is incident on the surface of seperation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the velocity of light in the medium?
View SolutionConsider a ray of light passing from one medium to another. If the angle of refraction is less than the angle of incidence, will the speed of light in the second medium be less or more than that in the first medium?
View Solution
