Two thin converging lenses are placed on a common axis, so that the centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
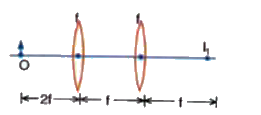
The image formed by first lens will be at distance 2f with lateral magnification m1=−1. For second lens this image will behave as a virtual object. Using the lens formula, 1v−1u=1f we have 1v−1f=1f
∴v=f2,m2=v2u2=(f/2)f=12
therefore , final image ( real is formed at a distance f/2 right from the second lens with total lateral magnification
m=m1×m2=(−1)×(12)=−12
Topper's Solved these Questions
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (LONG ANSWER QUESTIONS )
Explore 9 Videos
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (SHORT ANSWER QUESTIONS )
Explore 24 Videos
- PRACTICAL PHYSICSBook:AAKASH SERIESChapter:PRACTICAL PHYSICSExercise:LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
Explore 4 Videos
- SEMICONDUCTOR DEVICESBook:AAKASH SERIESChapter:SEMICONDUCTOR DEVICESExercise:EXERCISE - III
Explore 3 Videos
Similar Questions
Knowledge Check
An object is placed at a distance of 1.5m from a screen and a convex lens is interposed between them. The magnification produced is 4. What is the focal length of the lens ?
A1mB0.5mC0.24mD2m
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionAn object is placed in front of a converging lens at a distance greater than twice the focal length of the lens. Draw a ray diagram to show the formation of the image.
View SolutionWhen an object is at distances x and y from a lens, a real image and a virtual image is formed respectively having same magnification. The focal length of the lens is
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionAn object is placed at a distance u from an equiconvex lens such that the distannce between the object and its real image is minimum. The focal length of the lens is f. The value of u is
View SolutionThe graph shows how the magnification m produced by a thin lens varies with image distance v. What is the focal length of the lens used?
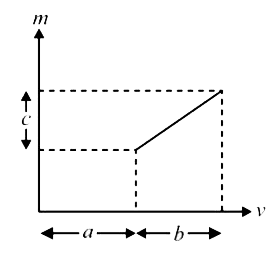
View Solution