There is a dust particle in a glass slab of thickness t and refractive index μ=1.5. When seen from one side of the slab, the dust particle appears at a distance 6 cm. From opposite side it appears at 4 cm. Find the thickness t of the glass slab.
To find the thickness t of the glass slab, we will use the concept of apparent depth and real depth in optics. Given the refractive index μ=1.5, we can set up the equations based on the information provided.
1. Define Variables:
- Let X be the real depth of the dust particle from the first surface of the glass slab.
- The thickness of the glass slab is t.
- Therefore, the real depth from the second surface is t−X.
2. Use the Refractive Index for the First Surface:
- When viewed from the first surface, the apparent depth is given as 6 cm.
- The relationship between real depth and apparent depth is given by:
μ=Real DepthApparent Depth
- For the first surface:
1.5=X6
- Rearranging gives:
X=1.5×6=9 cm
3. Use the Refractive Index for the Second Surface:
- When viewed from the second surface, the apparent depth is given as 4 cm.
- For the second surface:
1.5=t−X4
- Rearranging gives:
t−X=1.5×4=6 cm
4. Substituting the Value of X:
- We found X=9 cm from the first surface.
- Substitute X into the equation from the second surface:
t−9=6
- Solving for t:
t=6+9=15 cm
5. Conclusion:
- The thickness t of the glass slab is 15 cm.
Final Answer:
The thickness t of the glass slab is 15 cm.
- Let X be the real depth of the dust particle from the first surface of the glass slab.
- The thickness of the glass slab is t.
- Therefore, the real depth from the second surface is t−X.
- When viewed from the first surface, the apparent depth is given as 6 cm.
- The relationship between real depth and apparent depth is given by:
μ=Real DepthApparent Depth
- For the first surface:
1.5=X6
- Rearranging gives:
X=1.5×6=9 cm
- When viewed from the second surface, the apparent depth is given as 4 cm.
- For the second surface:
1.5=t−X4
- Rearranging gives:
t−X=1.5×4=6 cm
- We found X=9 cm from the first surface.
- Substitute X into the equation from the second surface:
t−9=6
- Solving for t:
t=6+9=15 cm
- The thickness t of the glass slab is 15 cm.
The thickness t of the glass slab is 15 cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)
57 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III
3 Videos
Similar Questions
There is a small black dot at the centre C of a solid glass sphere of refractive index μ. When seen from outside, the dot will appear to be located
View SolutionA small ink dot on a paper is viewed through a glass slab of thickness 10cm and refractive index 1.5. By what distance would the dot appear to be raised?
View SolutionA glass slab of thickness 3 cm and refractive index 3/2 is placed on ink mark on a piece of paper. For a person looking at the mark at a distance 2 cm above it, the distance of the mark will appear to be in cm
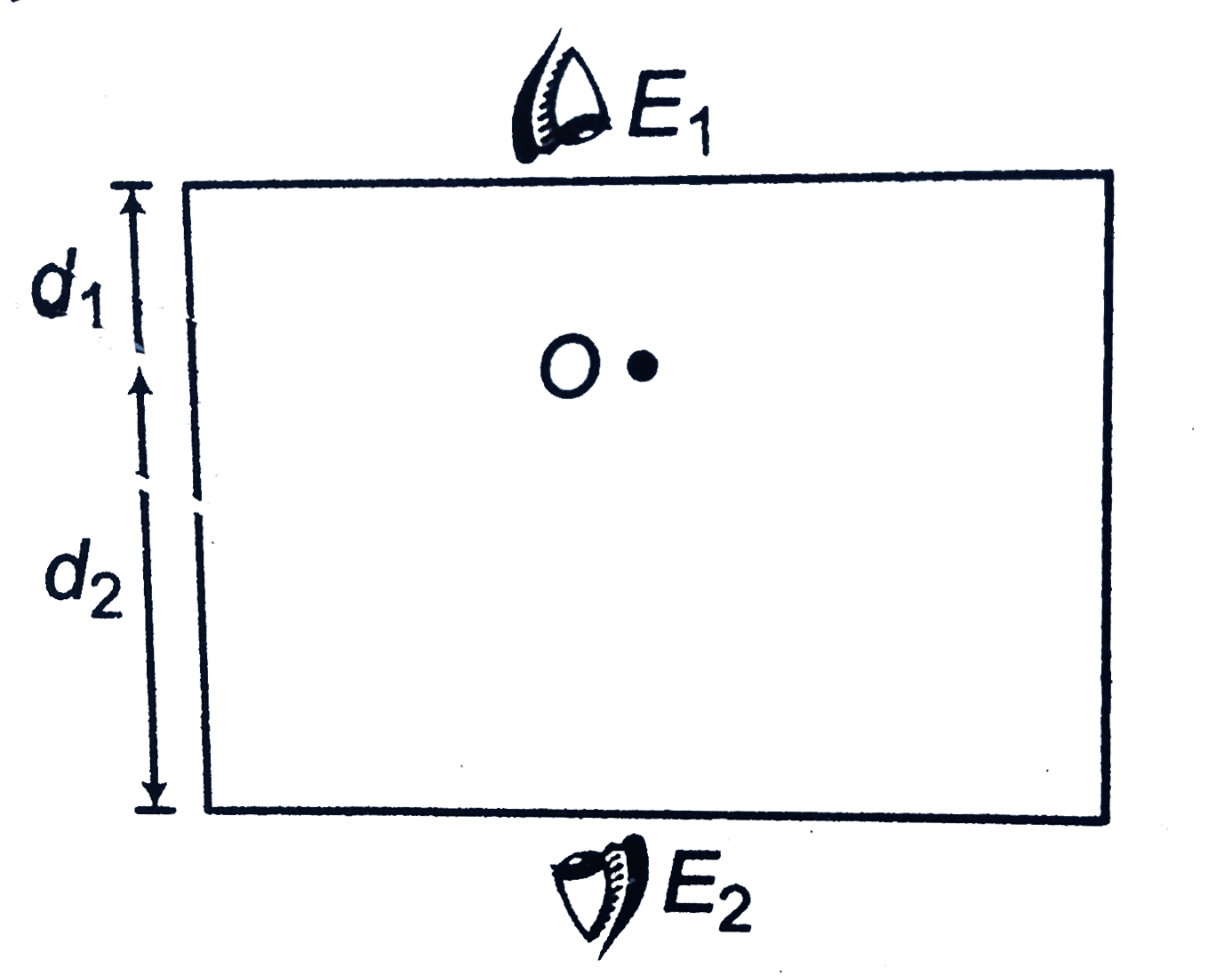
View SolutionRefractive index of the glass slab is 1.5. There is a point object O inside the slab as shown. To eyeE1 object appears at a distance of 6cm (From the top surface) and to eye E2 it appears at a distance of 8cm (from the bottom surface). Find thickness of the glass slab.
View SolutionAn object is seen through a glass slab of thickness 36cm and refractive index 3/2. The observer, and the slab are dipped in water (μ=4/3). The shift produced in the position of the object is
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionA ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
View SolutionIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
View SolutionA ray of light is incident normally on a glass slab of thickness 5 cm and refractive index 1.6. The time taken to travel by a ray from source to surface of slab is same as to travel through glass slab. The distance of source from the surface is
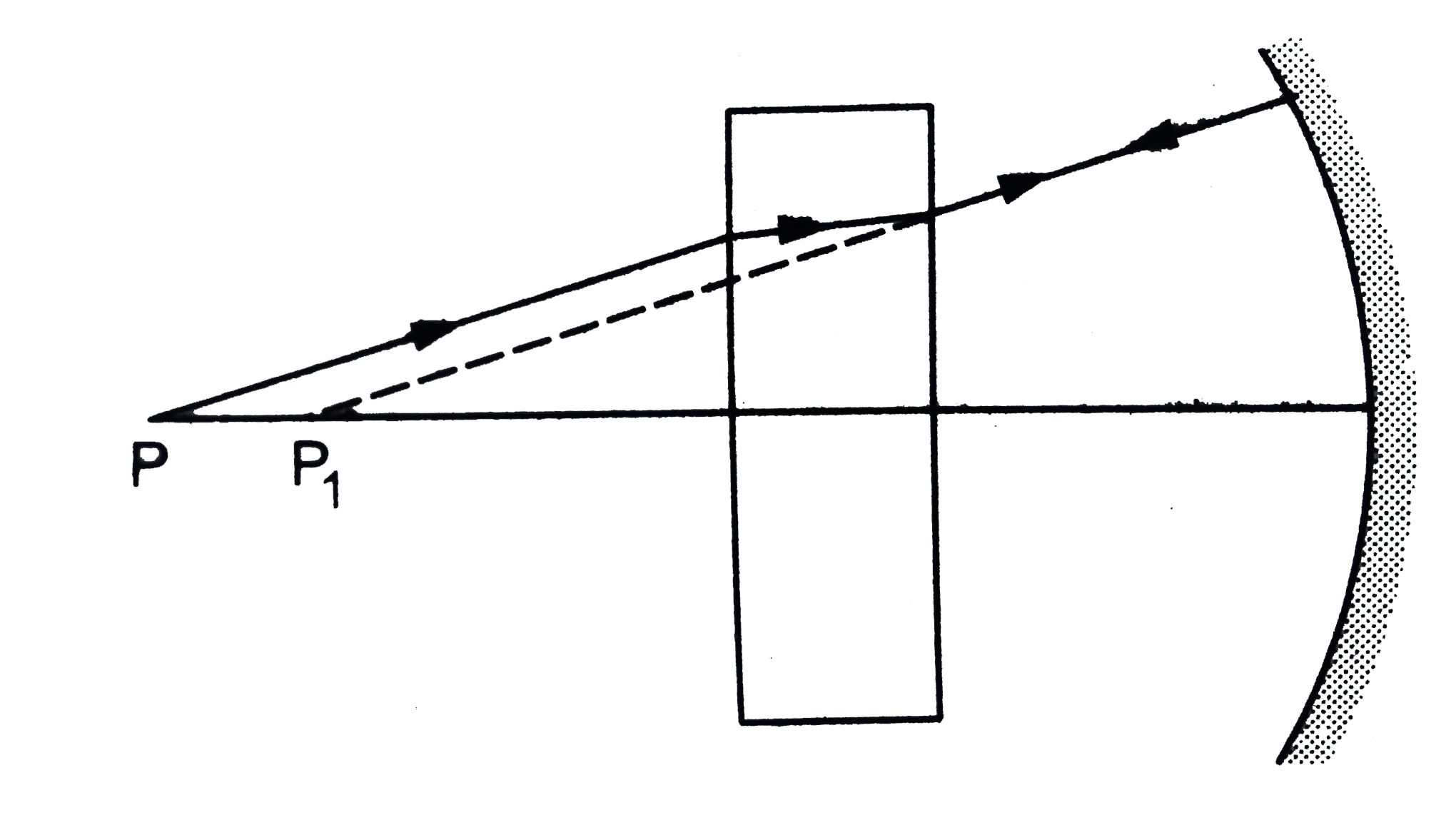
View SolutionAn object is placed 21 cm in fron of a concave mirror of radius of curvature 20 cm.A glass slab of thicknes 3 cm and refractive index 1.5 is palced close to the mirror in the space between the object and the mirror. Find the position of the final image fromed. The distance of the nearer surface of the slab from the mirror is 10 cm.
View Solution
