A parallel beam of light is incident on a rectangle transparent plate of thickness 8 cm. The angle of incidence and refraction of the beam is 60∘and30∘ respectively. Find the lateral shift.
To find the lateral shift of a parallel beam of light incident on a rectangular transparent plate, we can follow these steps:
Step 1: Identify the given values
- Thickness of the plate (t) = 8 cm
- Angle of incidence (i) = 60°
- Angle of refraction (r) = 30°
Step 2: Use the formula for lateral shift
The formula for lateral shift (l) is given by:
l=t⋅sin(i−r)cos(r)
Step 3: Substitute the values into the formula
Substituting the known values into the formula:
l=8cm⋅sin(60°−30°)cos(30°)
Step 4: Calculate the angles
Calculate 60°−30°:
60°−30°=30°
Step 5: Find the sine and cosine values
Now, we need the sine and cosine values:
- sin(30°)=12
- cos(30°)=√32
Step 6: Substitute these values back into the formula
Now substitute these values into the equation:
l=8cm⋅12√32
Step 7: Simplify the expression
This simplifies to:
l=8cm⋅1√3
Step 8: Calculate the lateral shift
Now calculate the final value:
l=8√3cm
Step 9: Approximate the value
Using √3≈1.732:
l≈81.732≈4.61cm
Final Answer
The lateral shift l is approximately 4.61cm.
---
- Thickness of the plate (t) = 8 cm
- Angle of incidence (i) = 60°
- Angle of refraction (r) = 30°
The formula for lateral shift (l) is given by:
l=t⋅sin(i−r)cos(r)
Substituting the known values into the formula:
l=8cm⋅sin(60°−30°)cos(30°)
Calculate 60°−30°:
60°−30°=30°
Now, we need the sine and cosine values:
- sin(30°)=12
- cos(30°)=√32
Now substitute these values into the equation:
l=8cm⋅12√32
This simplifies to:
l=8cm⋅1√3
Now calculate the final value:
l=8√3cm
Using √3≈1.732:
l≈81.732≈4.61cm
The lateral shift l is approximately 4.61cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)
57 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III
3 Videos
Similar Questions
A ray of light is incident on one face of a transparent slab of thickness 15 cm. The angle of incidence is 60∘. If the lateral displacement of the ray on emerging from the parallel plane is 5√3 cm, the refractive index of the material of the slab is
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View Solution
Knowledge Check
A parallel beam of sodium light of wavelength 6000Å is incident on a thin glass plate of μ=1.5, such that the angle of refraction in the plate is 60∘. The smallest thickness of the plate which will make it appear dark by reflected light is
A3926 Ã…B4353 Ã…C1396 Ã…D1921 Ã…A beam of light is incident at the polarizing angle of 35∘ on a certain glass plate. The refractive index of the glass plate is:
Asin35∘Btan35∘Ctan55∘Dsin55∘
A ray of light is incident on one face of a transparent glass slab of thickness 9cm at an angle of incidence 60∘. Lateral displacement of the ray on emerging from the opposite parallel face is 3√3cm. Refractive index of the material of slab is:
View SolutionA beam of light falls on a glass plate (μ=3/2) of thickness 6.0 cm at an angle of 60∘. Find the deflection of the beam on passing through the plate. (in cm).
View SolutionA parallel beam of light falls on a solid tranparent sphere.
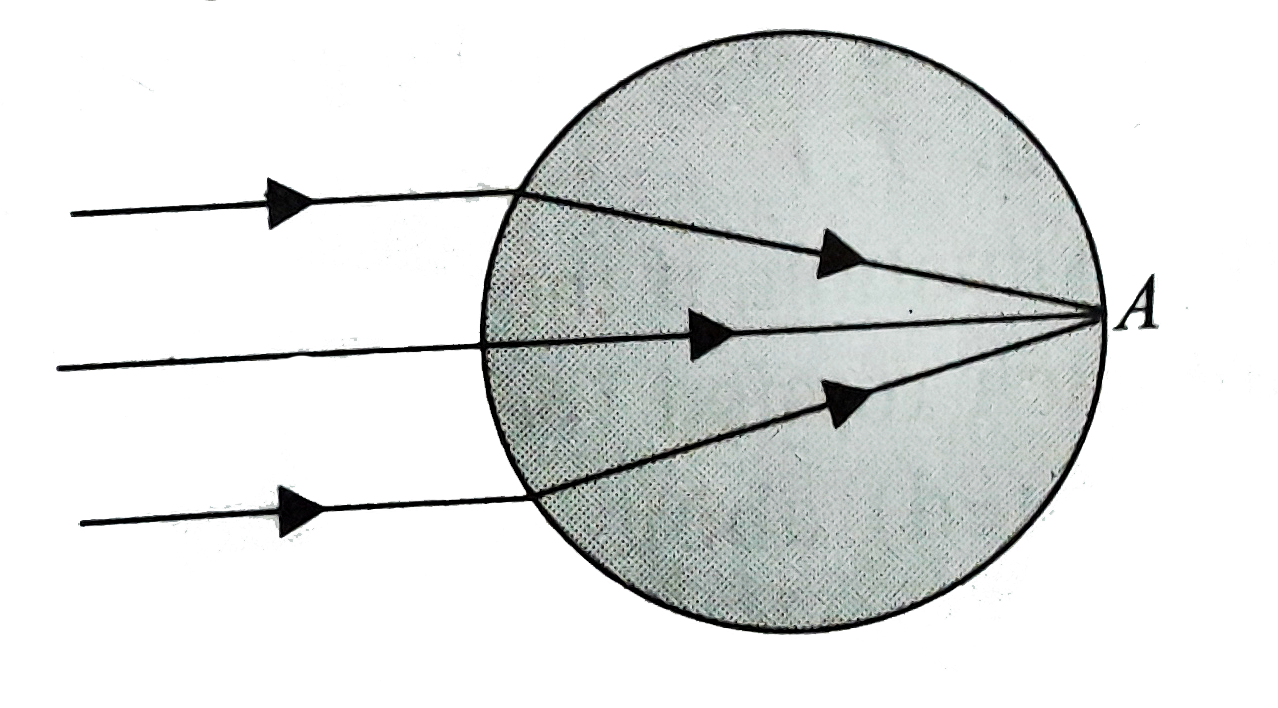
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA ray of light is incident on a transparent medium at polarizing angle. What is the angle between the reflected ray and the refracted ray .
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. By rotating the prism, the minimum angle of deviation is measured to be 40∘. What is the refractive index of the prism ? If the prism is placed in water (μ=1.33), predict the new angle of minimum deviation of the parallel beam. The refracting angle of prism is 60∘.
View SolutionA ray of light is incident on a rectangular plate at an angle of incidence 60∘. The light ray suffers a deviation which is 25% of the angle of incidence. The refractive index of the glass will be
View Solution
