A convex lens of focal length 10 cm. is used as a magnifying lens.
Where should the object be placed if the image is to be 30 cm from the lens?
To solve the problem, we need to find the object distance (u) for a convex lens given the focal length (f) and the image distance (v).
1. Identify the given values:
- Focal length of the convex lens, f=10cm (positive for convex lenses).
- Image distance, v=−30cm (negative because the image is on the same side as the object in a magnifying setup).
2. Use the lens formula:
The lens formula is given by:
1f=1v+1u
Rearranging this gives:
1u=1v−1f
3. Substitute the known values into the formula:
Plugging in the values for v and f:
1u=1−30−110
4. Calculate the right-hand side:
To perform the calculation, we need a common denominator:
1u=−130−330=−1−330=−430
5. Simplify the fraction:
1u=−215
6. Find the object distance (u):
Taking the reciprocal gives:
u=−152=−7.5cm
7. Conclusion:
The object should be placed at 7.5cm from the lens on the same side as the object (indicated by the negative sign).
Final Answer:
The object should be placed at 7.5cm from the lens.
- Focal length of the convex lens, f=10cm (positive for convex lenses).
- Image distance, v=−30cm (negative because the image is on the same side as the object in a magnifying setup).
The lens formula is given by:
1f=1v+1u
Rearranging this gives:
1u=1v−1f
Plugging in the values for v and f:
1u=1−30−110
To perform the calculation, we need a common denominator:
1u=−130−330=−1−330=−430
1u=−215
Taking the reciprocal gives:
u=−152=−7.5cm
The object should be placed at 7.5cm from the lens on the same side as the object (indicated by the negative sign).
The object should be placed at 7.5cm from the lens.
Topper's Solved these Questions
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (LONG ANSWER QUESTIONS )
Explore 9 Videos
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (SHORT ANSWER QUESTIONS )
Explore 24 Videos
- PRACTICAL PHYSICSBook:AAKASH SERIESChapter:PRACTICAL PHYSICSExercise:LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
Explore 4 Videos
- SEMICONDUCTOR DEVICESBook:AAKASH SERIESChapter:SEMICONDUCTOR DEVICESExercise:EXERCISE - III
Explore 3 Videos
Similar Questions
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A convex lens of a focal length 5 cm is used as a simple microscope. Where should an object be placed so that the image formed by it lies at the least distance of distinct vision (D = 25 cm) ?
View SolutionA convex lens has a focal length of 20 cm. It is used to form an image of an object placed 15 cm from lens. The image is
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
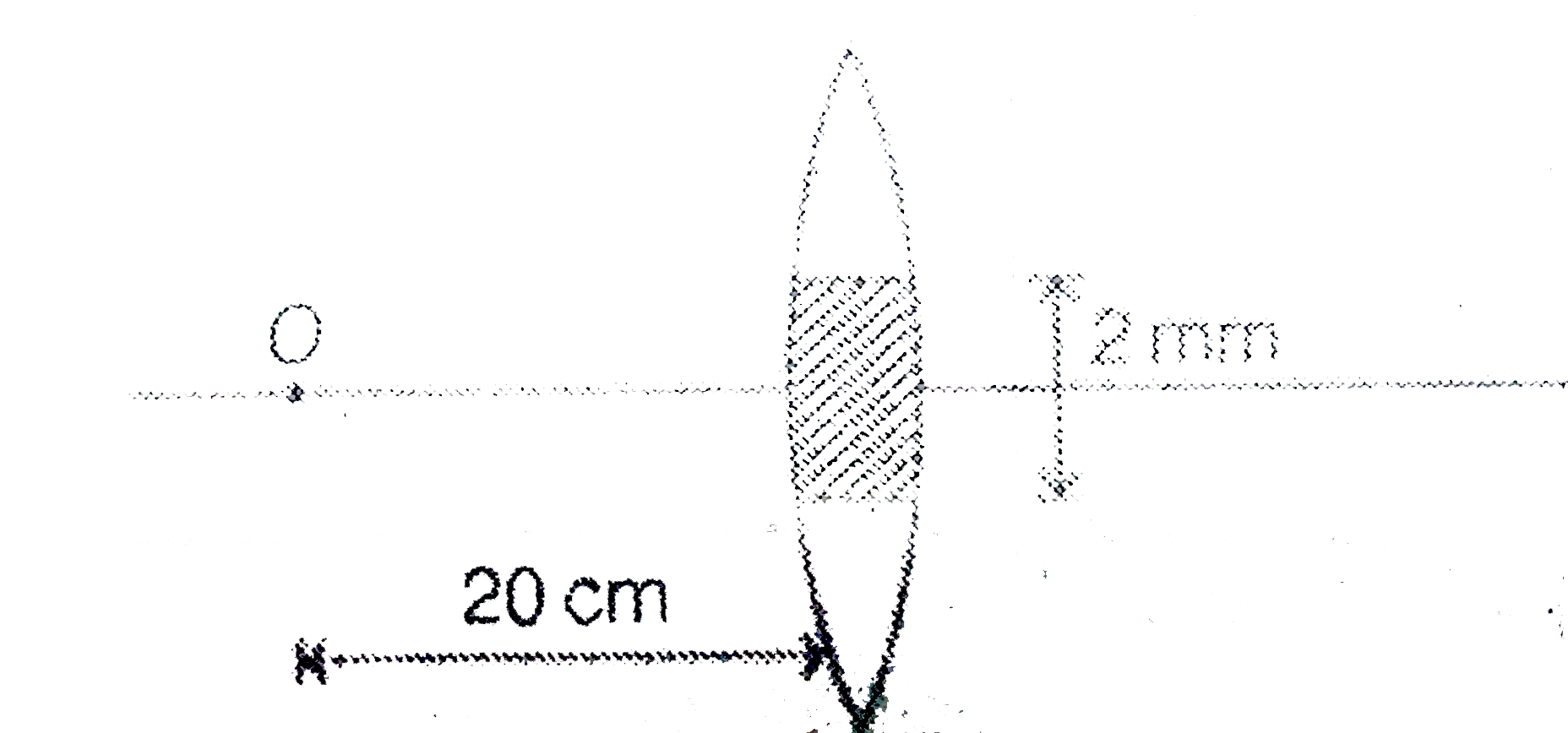
View SolutionA convex lens of focal length 30 cm produces 5 times magnified real image of an object. What is the object distance?
View SolutionIn an experiment for the determination of focal length of the convex mirror a convex lens of focal length 20cm is placed on the optical bench and an object pin is placed at a distance 30cm from the lens. When a convex mirror is introduced in between the lens and the real and inverted image of the object, the final image of object O is formed at O itself. If the distance between the lens and the mirror is 10cm, then the focal length of the mirror is
View SolutionA convex lens of focal length 30 cm , a concave lens of focal length 120 cm , and a plane mirror are arranged as shown . For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination , is a real image , at a distance of :
_E01_195_Q01.png)
|Focal length|=|Focal length|
= 30cm =120cm
_S01_267_Q02.png)
View SolutionA concave lens has focal length of 15 cm. At what distance should an object from the lens be placed so that it forms an image at 10 cm from the lens ? Also, find the magnification of the lens.
View Solution