Two identical coils, one of copper and the other of iron, are rotated with the same angular velocity ω in a uniform magnetic field. In which case the induced e.m.f. is more and why?
To determine which coil, copper or iron, has a greater induced electromotive force (e.m.f.) when rotated in a uniform magnetic field with the same angular velocity, we can analyze the situation step by step.
1. Understanding the Setup:
- We have two identical coils: one made of copper and the other made of iron.
- Both coils are rotated in a uniform magnetic field with the same angular velocity, denoted as ω.
2. Formula for Induced EMF:
- The induced e.m.f. (E) in a coil can be calculated using Faraday's law of electromagnetic induction, which states:
\(
E = -\frac{d\Phi}{dt}
\)
where \(\Phi\) is the magnetic flux through the coil.
3. Magnetic Flux Calculation:
- The magnetic flux (\(\Phi\)) through a coil is given by:
\(
\Phi = B \cdot A \cdot \cos(\theta)
\)
where:
- \(B\) is the magnetic field strength,
- \(A\) is the area of the coil,
- \(\theta\) is the angle between the magnetic field and the normal to the surface of the coil.
4. Differentiating Magnetic Flux:
- As the coils are rotated, the angle \(\theta\) changes with time, and we can express \(\theta\) as \(\theta = \omega t\).
- Therefore, the magnetic flux becomes:
\(
\Phi = B \cdot A \cdot \cos(\omega t)
\)
- To find the induced e.m.f., we differentiate the magnetic flux with respect to time:
\(
E = -\frac{d\Phi}{dt} = -\frac{d}{dt}(B \cdot A \cdot \cos(\omega t)) = B \cdot A \cdot \omega \cdot \sin(\omega t)
\)
5. Comparing Induced EMF in Both Coils:
- For both coils (copper and iron), the parameters \(B\), \(A\), and \(\omega\) are the same since they are identical coils and are subjected to the same magnetic field and angular velocity.
- Therefore, the induced e.m.f. for both coils is given by:
\(
E_{\text{copper}} = B \cdot A \cdot \omega \cdot \sin(\omega t)
\)
\(
E_{\text{iron}} = B \cdot A \cdot \omega \cdot \sin(\omega t)
\)
6. Conclusion:
- Since the induced e.m.f. is dependent on the same parameters for both coils, we conclude that:
\(
E_{\text{copper}} = E_{\text{iron}}
\)
- Thus, the induced e.m.f. is the same for both coils.
Final Answer:
The induced e.m.f. is the same for both the copper and iron coils when rotated in a uniform magnetic field with the same angular velocity.
- We have two identical coils: one made of copper and the other made of iron.
- Both coils are rotated in a uniform magnetic field with the same angular velocity, denoted as ω.
- The induced e.m.f. (E) in a coil can be calculated using Faraday's law of electromagnetic induction, which states:
\(
E = -\frac{d\Phi}{dt}
\)
where \(\Phi\) is the magnetic flux through the coil.
- The magnetic flux (\(\Phi\)) through a coil is given by:
\(
\Phi = B \cdot A \cdot \cos(\theta)
\)
where:
- \(B\) is the magnetic field strength,
- \(A\) is the area of the coil,
- \(\theta\) is the angle between the magnetic field and the normal to the surface of the coil.
- As the coils are rotated, the angle \(\theta\) changes with time, and we can express \(\theta\) as \(\theta = \omega t\).
- Therefore, the magnetic flux becomes:
\(
\Phi = B \cdot A \cdot \cos(\omega t)
\)
- To find the induced e.m.f., we differentiate the magnetic flux with respect to time:
\(
E = -\frac{d\Phi}{dt} = -\frac{d}{dt}(B \cdot A \cdot \cos(\omega t)) = B \cdot A \cdot \omega \cdot \sin(\omega t)
\)
- For both coils (copper and iron), the parameters \(B\), \(A\), and \(\omega\) are the same since they are identical coils and are subjected to the same magnetic field and angular velocity.
- Therefore, the induced e.m.f. for both coils is given by:
\(
E_{\text{copper}} = B \cdot A \cdot \omega \cdot \sin(\omega t)
\)
\(
E_{\text{iron}} = B \cdot A \cdot \omega \cdot \sin(\omega t)
\)
- Since the induced e.m.f. is dependent on the same parameters for both coils, we conclude that:
\(
E_{\text{copper}} = E_{\text{iron}}
\)
- Thus, the induced e.m.f. is the same for both coils.
The induced e.m.f. is the same for both the copper and iron coils when rotated in a uniform magnetic field with the same angular velocity.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problems (Level-I)
28 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problems (Level-II)
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Short Answer Questions)
21 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
Similar Questions
Two identical loops , one of copper and the other of aluminium , are rotated with the same angular speed in the magnetic field . Compare (i) the induced emf and (ii) the current produced in the two coils .
Justify your answer .
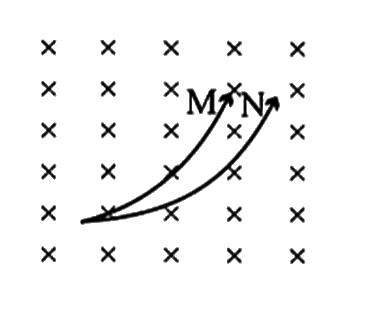
View SolutionTwo charged particle M and N are projected with same velocity in a uniform magnetic field. Then M and N respectively.
View SolutionA glass rod of length l moves with velocity v in a uniform magnetic field B. What is the e.m.f induced in the rod?
View SolutionTwo wires, one of copper and the other of iron, are of the same length and same radius. Which will have more resistance ? Give reason.
View SolutionA coil of N turns and mean cross-sectional area A is rotating with uniform angular velocity ω about an axis at right angle to uniform magnetic field B. The induced emf E in the coil will be
View SolutionIn the above question if the coil rotates with a constant angular velocity ω, the EMF induced in it
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
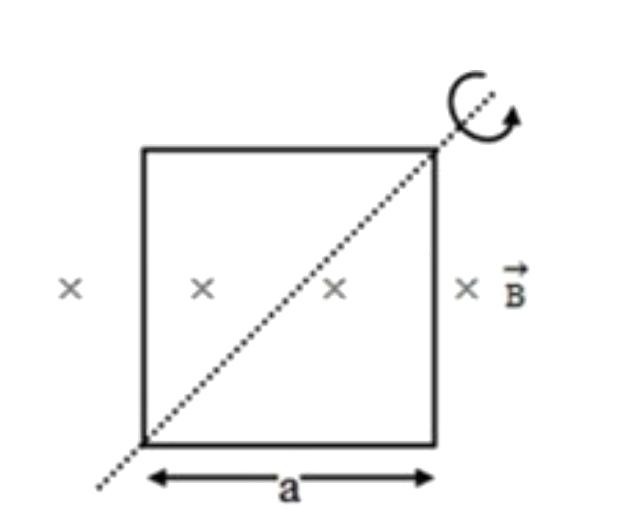
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

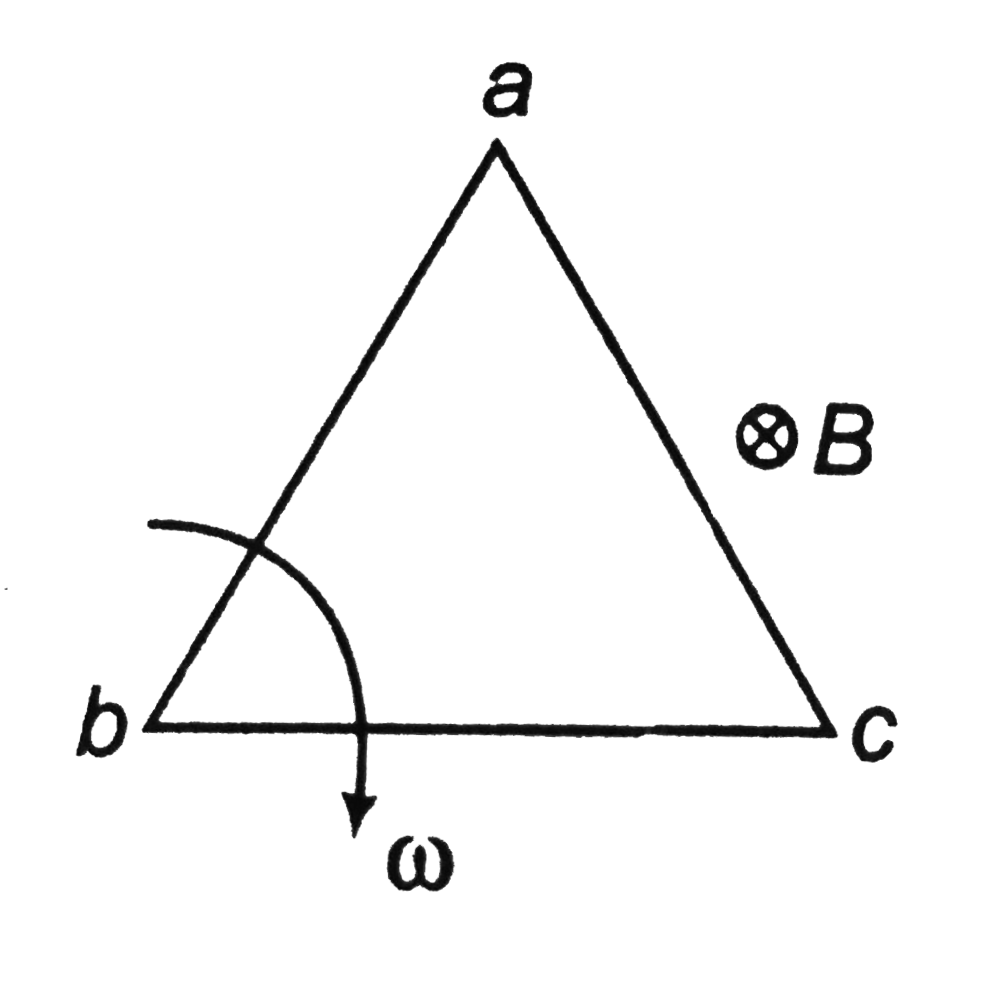
View SolutionAn equilateral triangular conducting frame is rotated with angular velocity ω in a uniform magnetic field B as shown. Side of triangle is l. choose the correct options
View Solution
