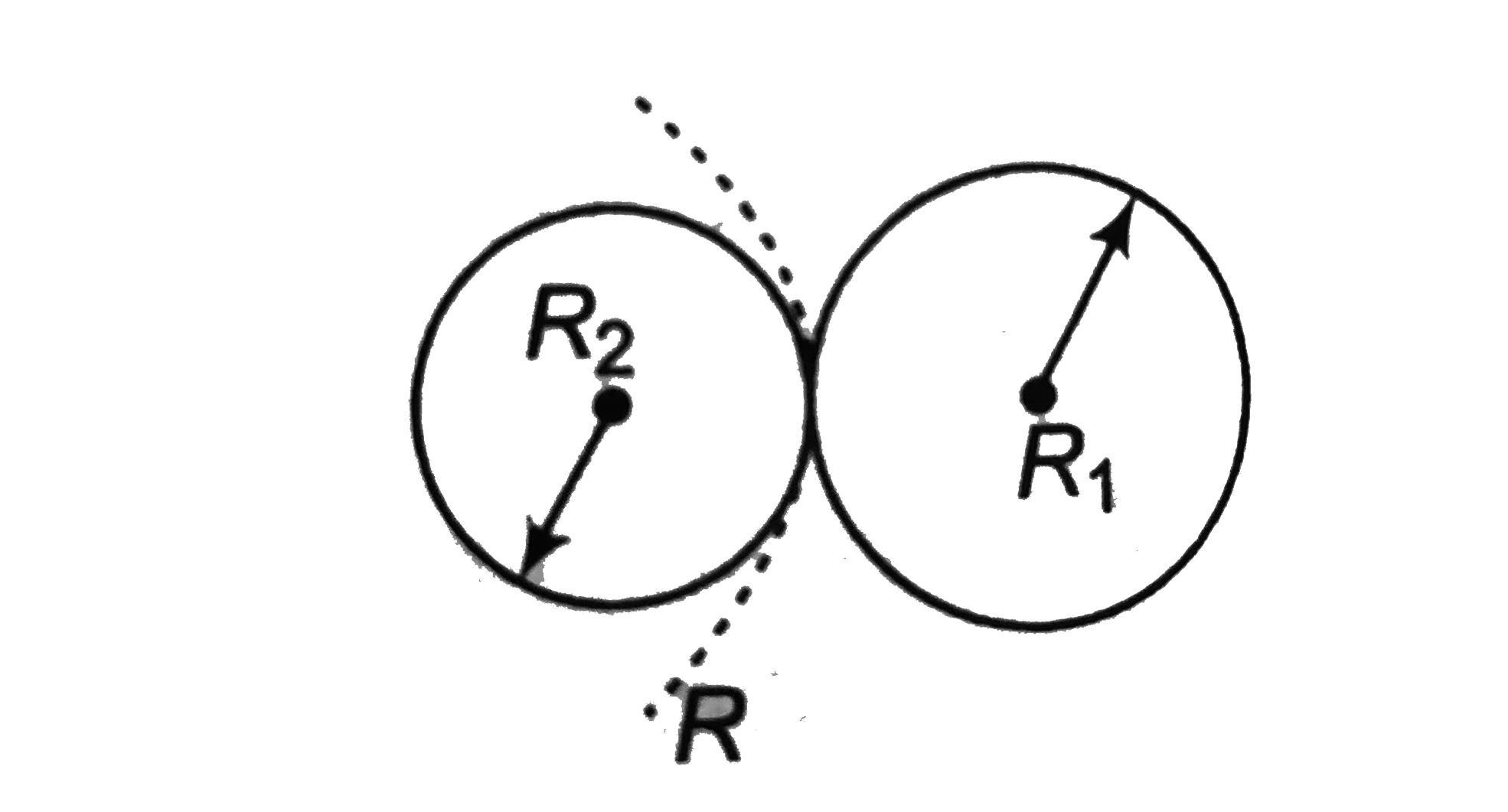
Two soap bubbles of different radii r1andr2 are in contact. Determine the radius of the interface.
To determine the radius of the interface between two soap bubbles of different radii r1 and r2, we can follow these steps:
Step 1: Understand the concept of excess pressure in soap bubbles
The excess pressure inside a soap bubble is given by the formula:
P=4σr
where P is the excess pressure, σ is the surface tension of the soap solution, and r is the radius of the bubble.
Step 2: Write the equations for the excess pressures
For the two soap bubbles with radii r1 and r2, the excess pressures P1 and P2 can be expressed as:
P1=4σr1
P2=4σr2
Step 3: Determine the resultant excess pressure
When the two bubbles are in contact, the resultant excess pressure P at the interface is the difference between the two pressures:
P=P1−P2=4σr1−4σr2
Step 4: Simplify the equation
We can factor out 4σ from the equation:
P=4σ(1r1−1r2)
Step 5: Relate the resultant pressure to the radius of the interface
Let R be the radius of the interface. The excess pressure at the interface can also be expressed as:
P=4σR
Step 6: Set the two expressions for pressure equal to each other
Now, we equate the two expressions for P:
4σR=4σ(1r1−1r2)
Step 7: Cancel 4σ from both sides
Assuming σ≠0, we can cancel 4σ:
1R=1r1−1r2
Step 8: Solve for R
Taking the reciprocal of both sides gives us:
R=r1r2r2−r1
Final Answer
Thus, the radius of the interface R between the two soap bubbles is:
R=r1r2r2−r1
---
The excess pressure inside a soap bubble is given by the formula:
P=4σr
where P is the excess pressure, σ is the surface tension of the soap solution, and r is the radius of the bubble.
For the two soap bubbles with radii r1 and r2, the excess pressures P1 and P2 can be expressed as:
P1=4σr1
P2=4σr2
When the two bubbles are in contact, the resultant excess pressure P at the interface is the difference between the two pressures:
P=P1−P2=4σr1−4σr2
We can factor out 4σ from the equation:
P=4σ(1r1−1r2)
Let R be the radius of the interface. The excess pressure at the interface can also be expressed as:
P=4σR
Now, we equate the two expressions for P:
4σR=4σ(1r1−1r2)
Assuming σ≠0, we can cancel 4σ:
1R=1r1−1r2
Taking the reciprocal of both sides gives us:
R=r1r2r2−r1
Thus, the radius of the interface R between the two soap bubbles is:
R=r1r2r2−r1
Similar Questions
Knowledge Check
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2
Two soap bubbles of radii 2 cm and 3 cm are brought in contact. Find the radius of curvature (in cm) of the contact surface.
View SolutionUnder isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View SolutionTwo soap bubbles with radius 2r and 3r come in contact. Their common surface has a radius of curvature nr, then find the value of n
View SolutionTwo soap bubbles coalesce.It noticed that, whilst joined together, the radii of the two bubbles are a and b where a>b.Then the radius of curvature of interface between the two bubbles will be
View SolutionTwo soap bubbles of radii r1 and r2 equal to 4 cm and 5 cm are touching each other over a common surface S1S2 (shown in figure). Its radius will be
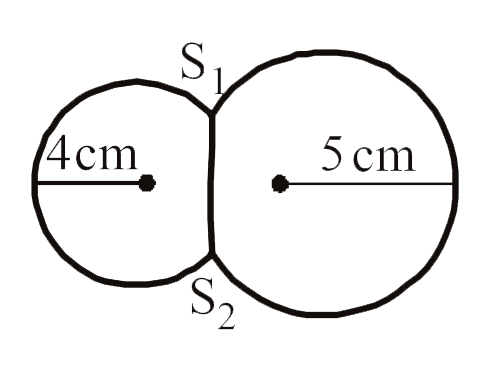
View SolutionProve that if two bubbles of radii r1 and r2 coalesce isothermally in vacuum then the radius of new bubble will be r=√r21+r22
View SolutionTwo soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View Solution

 .
.