Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
The correct Answer is:A, B, C, D
To find the surface tension of the soap in terms of the given parameters when two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r under isothermal conditions, we can follow these steps:
Step 1: Understand the excess pressure in soap bubbles
The excess pressure inside a soap bubble is given by the formula:
Pi=P0+4TR
where Pi is the internal pressure of the bubble, P0 is the external pressure, T is the surface tension, and R is the radius of the bubble.
Step 2: Write the equations for the two initial bubbles
For the two bubbles with radii r1 and r2, the internal pressures can be expressed as:
P1=P0+4Tr1
P2=P0+4Tr2
Step 3: Write the equation for the final bubble
After coalescing, the new bubble has a radius r and its internal pressure is:
P=P0+4Tr
Step 4: Apply the principle of conservation of volume
The total volume of the two smaller bubbles must equal the volume of the larger bubble:
43πr31+43πr32=43πr3
This simplifies to:
r31+r32=r3
Step 5: Set up the equation for pressures
Using the pressures from the bubbles, we can write:
P1V1+P2V2=PV
Substituting the volumes and pressures:
(P0+4Tr1)43πr31+(P0+4Tr2)43πr32=(P0+4Tr)43πr3
Step 6: Simplify the equation
Eliminating 43π from both sides:
(P0+4Tr1)r31+(P0+4Tr2)r32=(P0+4Tr)r3
Step 7: Expand and rearrange the equation
Expanding the left-hand side:
P0r31+4Tr1r31+P0r32+4Tr2r32=P0r3+4Trr3
Combining like terms gives:
P0(r31+r32)+4T(r31r1+r32r2)=P0r3+4Tr3r
Step 8: Solve for T
Rearranging to isolate T:
4T(r21+r22)=P0(r3−r31−r32)
Thus,
T=P0(r3−r31−r32)4(r21+r22)
Final Result
The surface tension T of the soap in terms of the given parameters is:
T=P0(r3−r31−r32)4(r21+r22)
The excess pressure inside a soap bubble is given by the formula:
Pi=P0+4TR
where Pi is the internal pressure of the bubble, P0 is the external pressure, T is the surface tension, and R is the radius of the bubble.
For the two bubbles with radii r1 and r2, the internal pressures can be expressed as:
P1=P0+4Tr1
P2=P0+4Tr2
After coalescing, the new bubble has a radius r and its internal pressure is:
P=P0+4Tr
The total volume of the two smaller bubbles must equal the volume of the larger bubble:
43πr31+43πr32=43πr3
This simplifies to:
r31+r32=r3
Using the pressures from the bubbles, we can write:
P1V1+P2V2=PV
Substituting the volumes and pressures:
(P0+4Tr1)43πr31+(P0+4Tr2)43πr32=(P0+4Tr)43πr3
Eliminating 43π from both sides:
(P0+4Tr1)r31+(P0+4Tr2)r32=(P0+4Tr)r3
Expanding the left-hand side:
P0r31+4Tr1r31+P0r32+4Tr2r32=P0r3+4Trr3
Combining like terms gives:
P0(r31+r32)+4T(r31r1+r32r2)=P0r3+4Tr3r
Rearranging to isolate T:
4T(r21+r22)=P0(r3−r31−r32)
Thus,
T=P0(r3−r31−r32)4(r21+r22)
The surface tension T of the soap in terms of the given parameters is:
T=P0(r3−r31−r32)4(r21+r22)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
21 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Two soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View Solution
Knowledge Check
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2The radii of two soap bubbles are r1andr2(r2<r1). They meet to produce a double bubble. The radius of their common interface is
Ar1r2r1+r2Br1+r22Cr1r2r1−r2Dr2−r1
Two soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
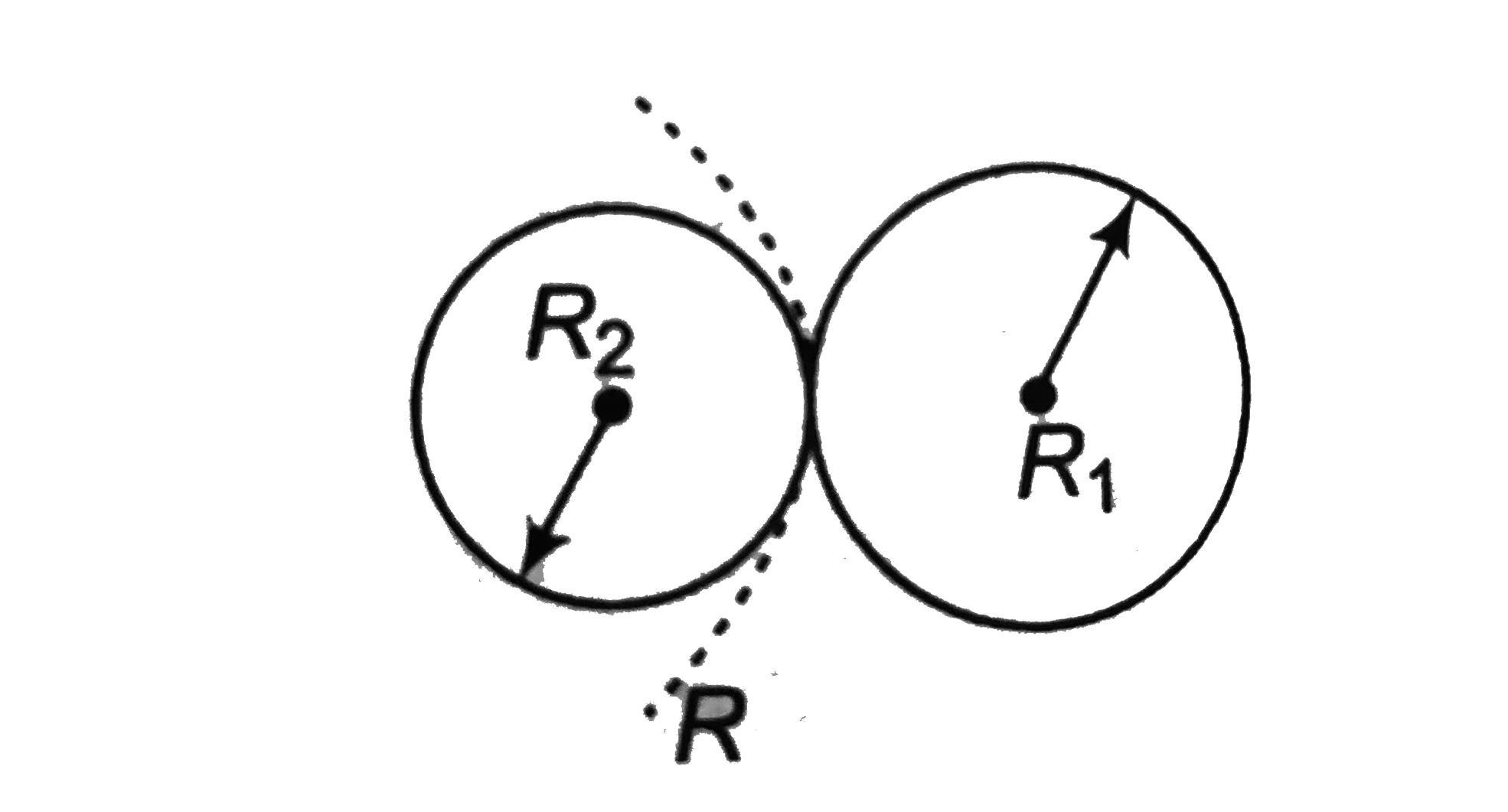 .
.
View SolutionAir is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution is S, the work done in the process is
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionTwo identical soap bubbles each of radius r and of the same surface tension T combine to form a new soap bubble of radius R. The two bubbles contain air at the same temperature. If the atmospheric pressure is p0 then find the surface tension T of the soap solution in terms of p0, r and R. Assume process is isothermal.
View SolutionA soap bubble of radius 'r' is blown up to form a bubble of radius 2r under isothemal conditions. If σ be the surface tension of soap solution , the energy spent in doing so is
View SolutionTwo soap bubbles in vacuum of radius 3cm and4cm coalesce to form a single bubble, in same temperature. What will be the radius of the new bubble
View Solution
