The period T and mean distance R of a planet from the sun are related by
T2∝R2
T∝R3
T3∝R2
T2/3∝R
The correct Answer is:D
To solve the problem regarding the relationship between the period T and the mean distance R of a planet from the sun, we can use Kepler's Third Law of planetary motion. Here’s a step-by-step solution:
Step 1: Understand Kepler's Third Law
Kepler's Third Law states that the square of the orbital period T of a planet is directly proportional to the cube of the semi-major axis (mean distance) R of its orbit. Mathematically, this can be expressed as:
T2∝R3
Step 2: Introduce a Constant of Proportionality
To express this relationship in an equation, we introduce a constant k:
T2=kR3
Step 3: Rearranging the Equation
To analyze the relationship between T and R, we can rearrange the equation. Taking the cube root of both sides gives:
T2/3=k′R
where k′=k1/3.
Step 4: Interpret the Result
This shows that the period T raised to the power of 23 is directly proportional to the mean distance R:
T2/3∝R
Conclusion
Thus, we conclude that the period T and the mean distance R of a planet from the sun are related by the equation:
T2/3=kR
where k is a constant.
Kepler's Third Law states that the square of the orbital period T of a planet is directly proportional to the cube of the semi-major axis (mean distance) R of its orbit. Mathematically, this can be expressed as:
T2∝R3
To express this relationship in an equation, we introduce a constant k:
T2=kR3
To analyze the relationship between T and R, we can rearrange the equation. Taking the cube root of both sides gives:
T2/3=k′R
where k′=k1/3.
This shows that the period T raised to the power of 23 is directly proportional to the mean distance R:
T2/3∝R
Thus, we conclude that the period T and the mean distance R of a planet from the sun are related by the equation:
T2/3=kR
where k is a constant.
Similar Questions
A planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
View SolutionThe ratio of mean distances of three planets from the sun are 0.5:1:1:5, then the square of time periods are in the ratio of
View SolutionWhich of the following graphs between the square of the time period and cube of the distance of the planet from the sun is correct ?
View SolutionWhich of the following graphs between the square of the time period and cube of the distance of the planet from the sun is correct ?
View SolutionA planet of mass m moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are r1 and r2, respectively. Find the relation between the time period of the planet in terms of r1 and r2.
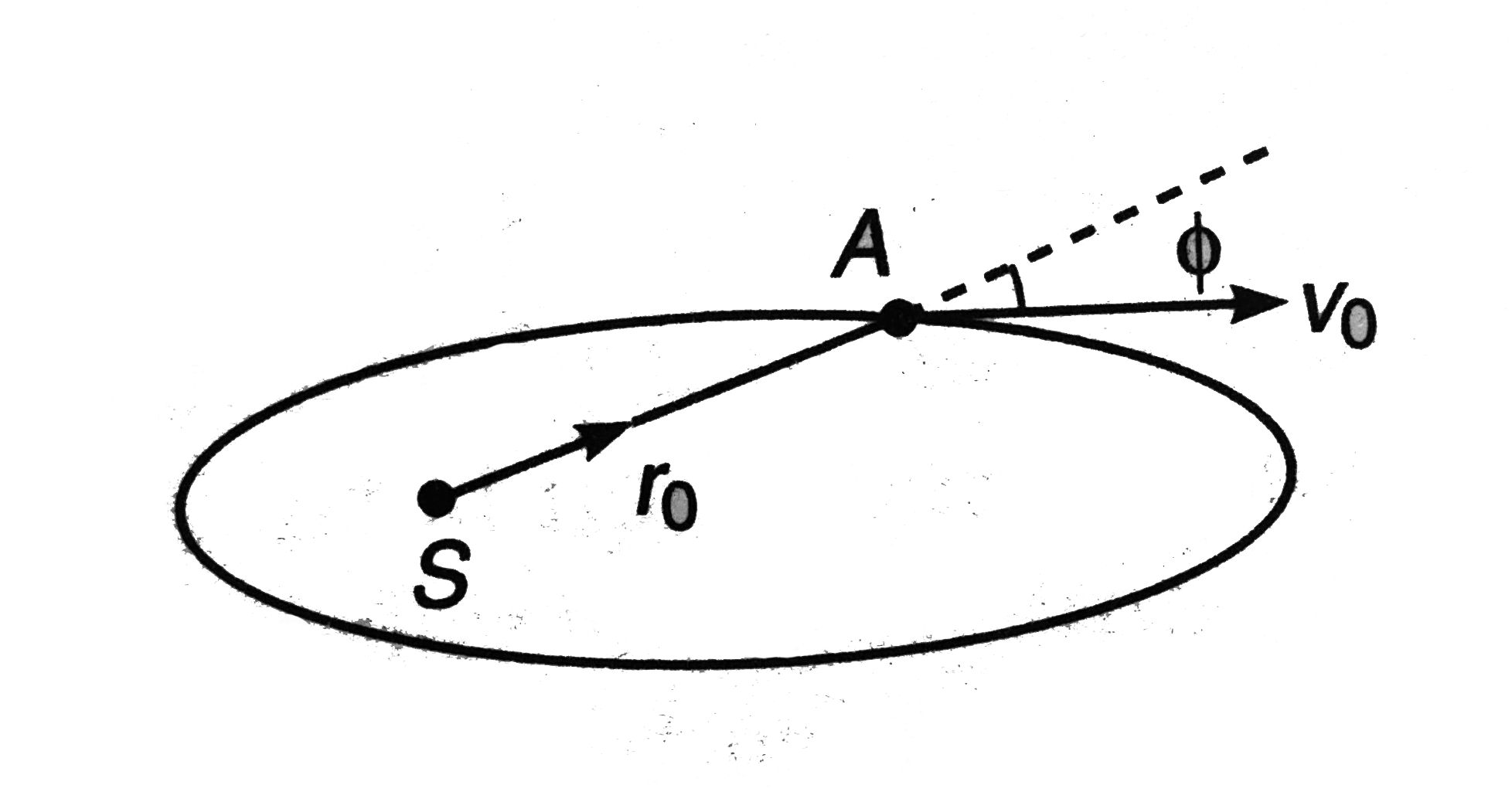
View SolutionFind the maximum and minimum distances of the planet A from the sun S, if at a certain moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
View SolutionThe minimum and maximum distances of a planet revolving around sun are r and R . If the minimum speed of planet of its trajectory is v0 , its maximum speed will be
View SolutionThe time of revolution of planet A round the sun is 8 times that of another planet B. The distance of planet A from the sun is how many times the distance of B from the sun
View SolutionThe largest and the shortest distance of the earth from the sun are r1 and r2, its distance from the sun when it is at the perpendicular to the major axis of the orbit drawn from the sun
View SolutionThe solar constant is the amount of heat energy received per second per unit area of a perfectly black surface placed at a mean distance of the Earth form the Sun, in the absence of Earth's atmosphere, the surface being held perpendicular to the direction of Sun's rays. Its value is 1388W/m2. If the solar constant for the earth is 's'. The surface temperature of the sun is TK,D is the diameter of the sun, R is the mean distance of the Earth from the sun. The sun subtends a small angle 'theta' at the earth. Then correct options is/are:-
View Solution