For planets revolving round the sun, show that T2∝r3, where T is the time period of revolution of the planet and r is its distance from the sun.
(1) The centripetal force actiong on the planet revolving round the sun with orbital velocity 'v' is, F=mv2r
(2) Substitute, v=2πrT
where 'T' is the time period of revolution of the planet.
(3) The force of attraction between planet and sun is equal to GMmR2
Equate (1) and (3). Then obtain the relation T2∝r3 from the above solution.
Topper's Solved these Questions
Similar Questions
How does the period of revolution of a planet around the sun vary with its distance from the sun?
View SolutionConsider a planet of mass (m), revolving round the sun. The time period (T) of revolution of the planet depends upon the radius of the orbit (r), mass of the sun (M) and the gravitational constant (G). Using dimensional analysis, verify Kepler' third law of planetary motion.
View Solution
Knowledge Check
- Question 1 - Select One
For a planet revolving round the sun, when it is nearest to the sun
AK.E. is min and P.E. is max.Bboth K.E. and P.E. are minCK.E. is max. and P.E. is minDK.E. and P.E. are equal - Question 2 - Select One
If a and b are the nearest and farthest distances of a planet from the sun and the planet is revolving in an elliptical orbit, then square of the time period of revolution of that planets is directly proportional to
Aa3Bb3C(a+b)3D(a−b)3 - Question 3 - Select One
A planet is revolving around the sun in a circular orbit with a radius r. The time period is T .If the force between the planet and star is proportional to r−3/2 then the quare of time period is proportional to
Ar3/2Br2CrDr5/2
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
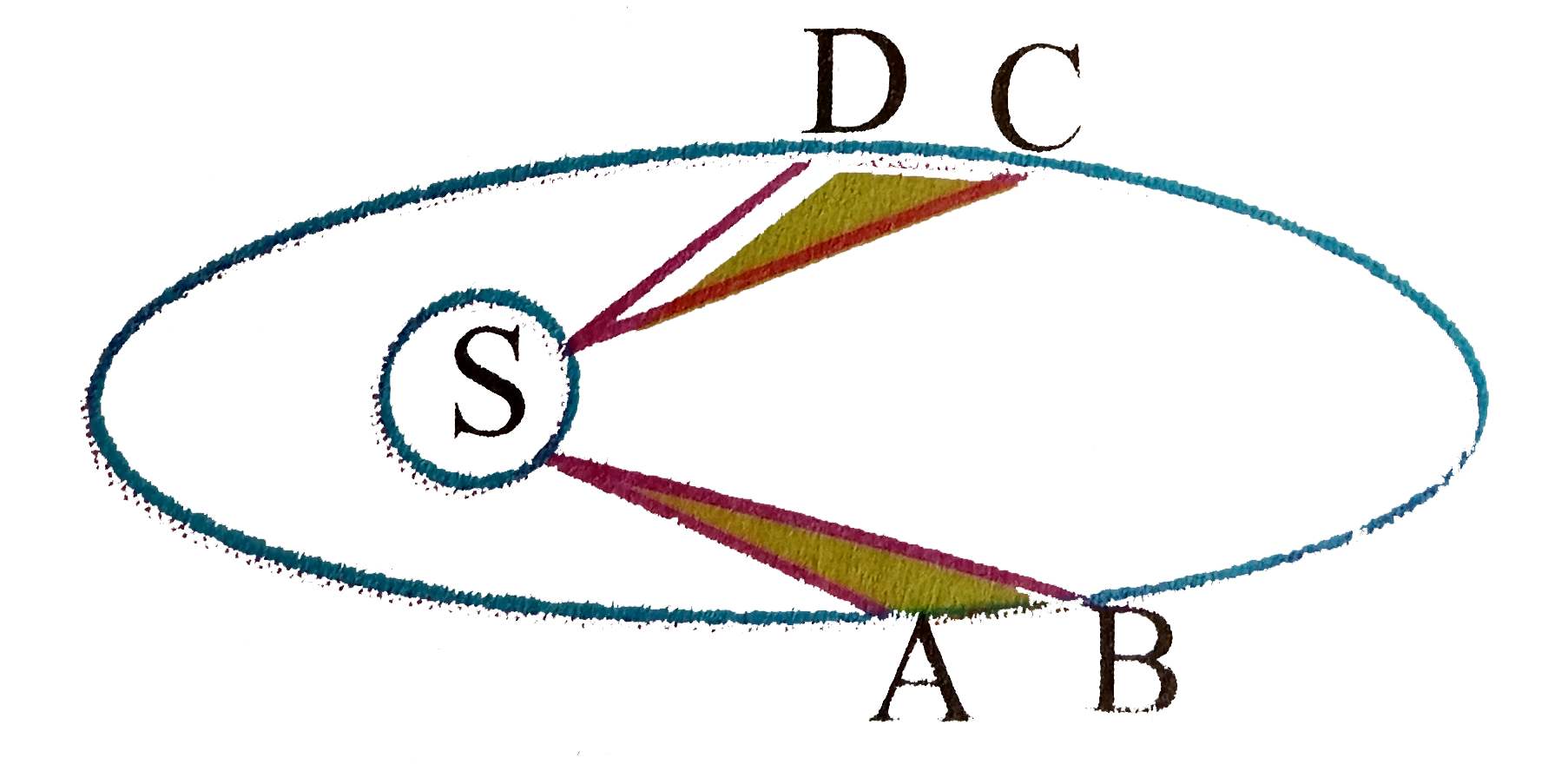 View Solution
View SolutionA planet is revolving around the sun. its distance from the sun at apogee is rA and that at perigee is rp. The masses of planet and sun are 'm' and M respectively, VA is the velocity of planet at apogee and VP is at perigee respectively and T is the time period of revolution of planet around the sun, then identify the wrong answer.
View SolutionIf a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the end of the minor axis and close to the sun is
View Solution

