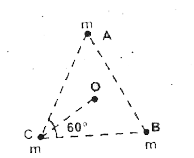
Three particles of identical masses .m. are kept at the vertices of an equilateral triangle of each side length.a.. Find the gravitational force of attraction on any one of the particles.
To find the gravitational force of attraction on any one of the particles placed at the vertices of an equilateral triangle, we can follow these steps:
1. Visualize the Setup:
- We have three identical masses (m) located at the vertices of an equilateral triangle with each side of length (a). Let's label the masses as m1, m2, and m3.
2. Identify the Forces:
- We need to calculate the gravitational force acting on one of the particles due to the other two. Let's calculate the force on m2 due to m1 and m3.
3. Calculate the Gravitational Force:
- The gravitational force between two masses is given by the formula:
F=Gm1m2r2
- For the forces acting on m2:
- The force due to m1 (let's call it F21) is:
F21=Gm2a2
- The force due to m3 (let's call it F23) is also:
F23=Gm2a2
4. Determine the Angles:
- Since the triangle is equilateral, the angle between the lines connecting m2 to m1 and m3 is 60∘.
5. Resolve the Forces:
- We need to resolve the forces F21 and F23 into their components. The horizontal (x) and vertical (y) components of these forces can be calculated as follows:
- The x-component of F21 is:
F21x=F21cos(60∘)=Gm2a2⋅12=Gm22a2
- The y-component of F21 is:
F21y=F21sin(60∘)=Gm2a2⋅√32=Gm2√32a2
- The x-component of F23 is:
F23x=F23cos(60∘)=Gm2a2⋅12=Gm22a2
- The y-component of F23 is:
F23y=F23sin(60∘)=Gm2a2⋅√32=Gm2√32a2
6. Calculate the Resultant Force:
- The total x-component of the force acting on m2 is:
Fnetx=F21x+F23x=Gm22a2+Gm22a2=Gm2a2
- The total y-component of the force acting on m2 is:
Fnety=F21y+F23y=Gm2√32a2+Gm2√32a2=Gm2√3a2
7. Combine the Components:
- The resultant gravitational force Fnet can be calculated using the Pythagorean theorem:
Fnet=√(Fnetx)2+(Fnety)2
Fnet=
⎷(Gm2a2)2+(Gm2√3a2)2
Fnet=√G2m4a4+3G2m4a4=√4G2m4a4=2Gm2a2
Final Answer:
The gravitational force of attraction on any one of the particles is:
Fnet=2Gm2a2
- We have three identical masses (m) located at the vertices of an equilateral triangle with each side of length (a). Let's label the masses as m1, m2, and m3.
- We need to calculate the gravitational force acting on one of the particles due to the other two. Let's calculate the force on m2 due to m1 and m3.
- The gravitational force between two masses is given by the formula:
F=Gm1m2r2
- For the forces acting on m2:
- The force due to m1 (let's call it F21) is:
F21=Gm2a2
- The force due to m3 (let's call it F23) is also:
F23=Gm2a2
- Since the triangle is equilateral, the angle between the lines connecting m2 to m1 and m3 is 60∘.
- We need to resolve the forces F21 and F23 into their components. The horizontal (x) and vertical (y) components of these forces can be calculated as follows:
- The x-component of F21 is:
F21x=F21cos(60∘)=Gm2a2⋅12=Gm22a2
- The y-component of F21 is:
F21y=F21sin(60∘)=Gm2a2⋅√32=Gm2√32a2
- The x-component of F23 is:
F23x=F23cos(60∘)=Gm2a2⋅12=Gm22a2
- The y-component of F23 is:
F23y=F23sin(60∘)=Gm2a2⋅√32=Gm2√32a2
- The total x-component of the force acting on m2 is:
Fnetx=F21x+F23x=Gm22a2+Gm22a2=Gm2a2
- The total y-component of the force acting on m2 is:
Fnety=F21y+F23y=Gm2√32a2+Gm2√32a2=Gm2√3a2
- The resultant gravitational force Fnet can be calculated using the Pythagorean theorem:
Fnet=√(Fnetx)2+(Fnety)2
Fnet=
⎷(Gm2a2)2+(Gm2√3a2)2
Fnet=√G2m4a4+3G2m4a4=√4G2m4a4=2Gm2a2
The gravitational force of attraction on any one of the particles is:
Fnet=2Gm2a2
Similar Questions
Three point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
Force acting on particle C, due to particle A and B
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.

The gravitational potential at O is
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree identical point objects each of mass m are placed at the vertices of an equilateral triange of side l. What is the gravitational potential at the centre of the equilateral triangle due to the point masses?
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View SolutionThree particles, each of mass 200 g are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis
a. joining two of the particles
b. passing through one of the particle perpendicular to the plane of the particles.
View SolutionThree particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
View Solution
