Three identical point objects each of mass m are placed at the vertices of an equilateral triange of side l. What is the gravitational potential at the centre of the equilateral triangle due to the point masses?
To find the gravitational potential at the center of an equilateral triangle due to three identical point masses located at its vertices, we can follow these steps:
Step 1: Understand the Configuration
We have three identical point masses, each of mass m, placed at the vertices of an equilateral triangle with side length l. The center of the triangle is also known as the centroid.
Step 2: Determine the Distance from the Centroid to the Vertices
The distance from the centroid (center) to any vertex of the equilateral triangle can be calculated using the formula for the centroid of a triangle. The centroid divides the median in the ratio 2:1. The length of the median m of an equilateral triangle is given by:
m=√32l
Thus, the distance d from the centroid to a vertex is:
d=23m=23(√32l)=l√33
Step 3: Calculate the Gravitational Potential due to One Mass
The gravitational potential V due to a point mass m at a distance d is given by:
V=−Gmd
Step 4: Calculate the Total Gravitational Potential at the Centroid
Since there are three identical masses, the total gravitational potential Vtotal at the centroid is the sum of the potentials due to each mass. Because gravitational potential is a scalar quantity, we can simply add them:
Vtotal=VA+VB+VC=−Gmd−Gmd−Gmd=−3Gmd
Substituting d=l√33:
Vtotal=−3Gml√33=−9Gml√3
Final Answer
Thus, the gravitational potential at the center of the equilateral triangle due to the three point masses is:
V=−9Gml√3
We have three identical point masses, each of mass m, placed at the vertices of an equilateral triangle with side length l. The center of the triangle is also known as the centroid.
The distance from the centroid (center) to any vertex of the equilateral triangle can be calculated using the formula for the centroid of a triangle. The centroid divides the median in the ratio 2:1. The length of the median m of an equilateral triangle is given by:
The gravitational potential V due to a point mass m at a distance d is given by:
Since there are three identical masses, the total gravitational potential Vtotal at the centroid is the sum of the potentials due to each mass. Because gravitational potential is a scalar quantity, we can simply add them:
Thus, the gravitational potential at the center of the equilateral triangle due to the three point masses is:
Similar Questions
Three mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?
View Solution
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
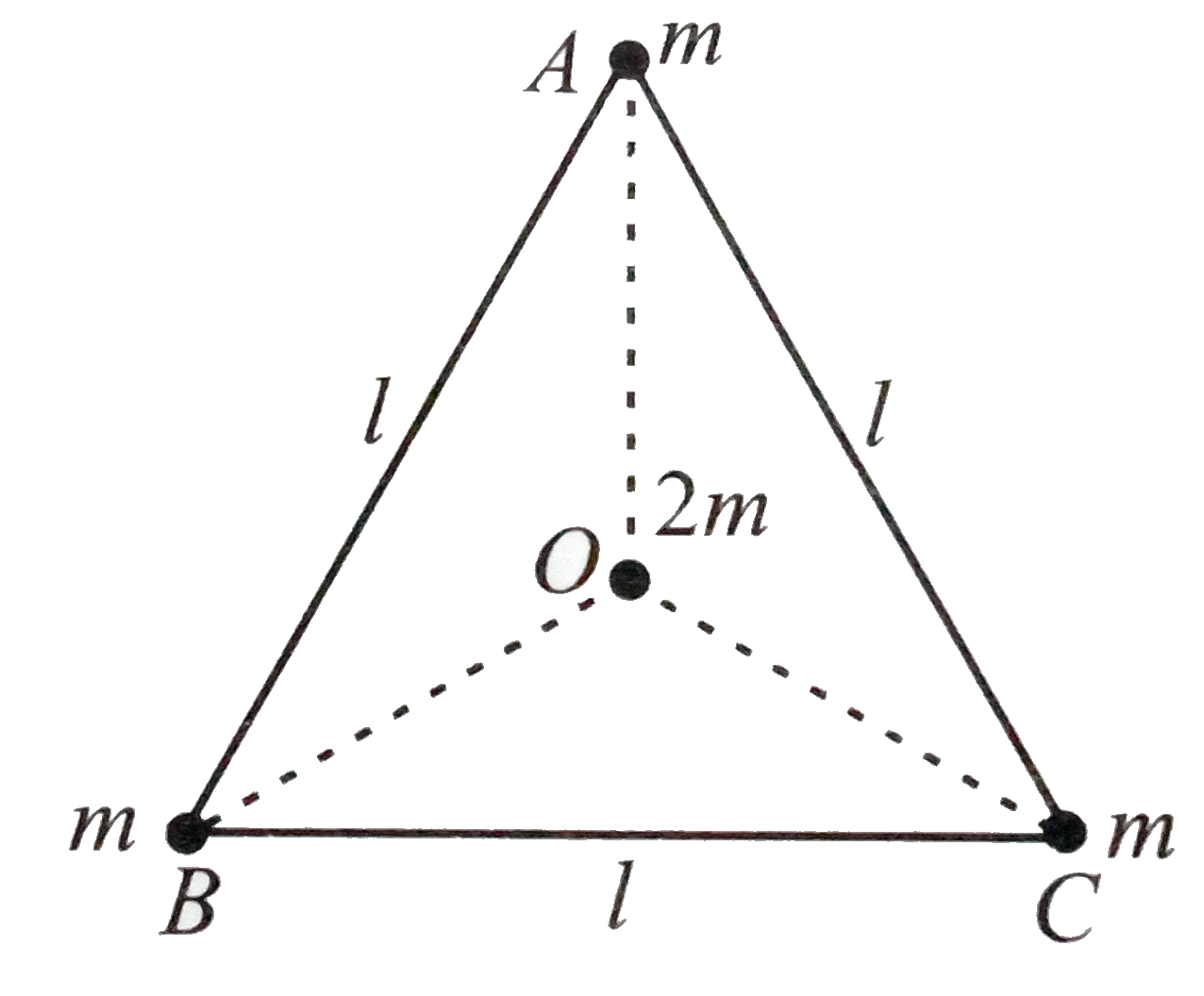 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Three particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionIf 3 charges are placed at the vertices of equilateral triangle of charge 'q' each. What is the net potential energy, if the side of equilateral Δ is lcm ?
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle of side 1 m, then the gravitational force on one of the masses due to other masses is (approx.)
View SolutionThree identical charges, each having a value 1.0×10−8C, are placed at the corners of an equilateral triangle of side 20 cm find the electric field and potential at the centre of the triangle.
View Solution
