Two steel rods and an aluminium rod of equal length l0 and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
At increased temperature, let Δl1andΔl2 be the increase in length of aluminium and steel respectively (if they are free).
Then Δl1=l0α1θandΔl2=l0α2θ
Suppose Δl1<Δl2
Therefore, the composite rod will increase in between Δl1andΔl2. Say it is Δl, where Δl1<Δl<Δl2 Due to this, aluminium rod has a length (Δl−Δl1) more than its natural length at temperature θ and steel rod (s) will have a length (Δl2−Δl) less than its natural length at temperature θ. Due to this, steel rods will exert force F2 on aluminium rod from two sides, which in equilibrium be balanced by internal restoring force F1. Thus,


∴Y1A(Δl−Δl1l0)=2Y2A(Δl2−Δll0)
Solving this we get, Δl=Y1Δl1+2Y2Δl2Y1+2Y2
= Y1l0α1θ+2Y2l0α2θY1+2Y2=l0θ(Y1α1+2Y2α2)Y1+2Y2
Similar Questions
Two steel rods and an aluminum rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminum and steel are αaandαs respectively. Young's modulus of aluminum is Ya and of steel is Ys.

View SolutionA steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5C−1.
View SolutionA steel rod is clamped at its two ends and rests on a fixes horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5∘C−1.
View SolutionA steel rod is clamped at its two ends and rests on a fixes horizontal base. The rod is unstrained at 20∘C. Find the longitudinal strain developed in the rod if the temperature rises to 50∘C. Coefficient of linear expansion of steel =1.2×10−5∘C−1.
View SolutionWhat should be the sum of lengths of an aluminium and steel rod at 0∘C is, so that all the temperature their difference in length is 0.25m. (Take coefficient of linear expansion for aluminium and steel at 0∘C as 22×10−6/.∘C and 11×10−5/.∘C respectively.)
View SolutionA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
View SolutionTwo rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
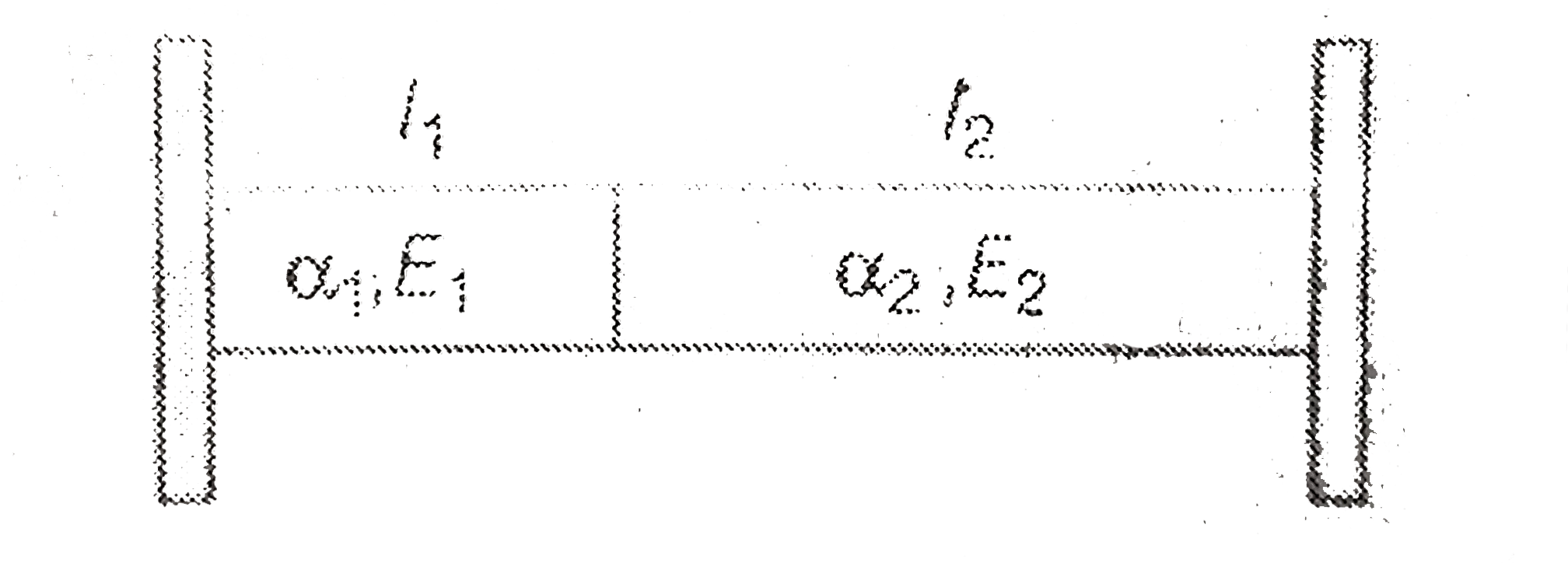
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_227_Q01.png)
If temperature of system is increased by ΔT then junction will not shift if -
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remian constant at any temperature then
View Solution