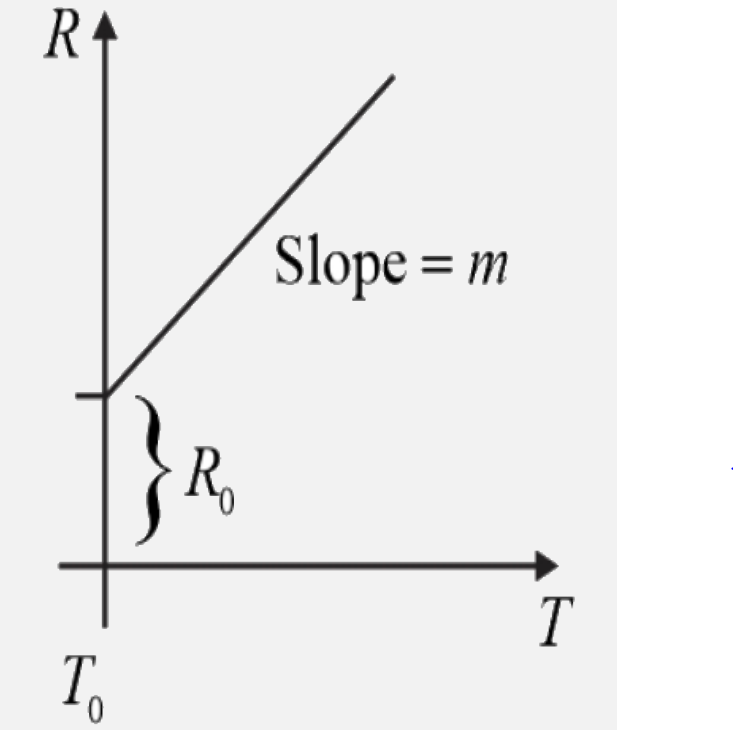
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
αA=3×10−6/∘C,500∘C
αA=3×10−6/∘C,222.22∘C
αA=27×10−6/∘C,500∘C
αA=27×10−6/∘C,222.22∘C
The correct Answer is:D
Slope of line A=(1006−1000)mmT∘C=ΔLΔT=LαA
i.e., 6Tmm/∘C=(1000mm)αA
similary for line B
2Tmm/∘C=(1002mm)αB
Dividing Eq. (i) by Eq. (ii)
3=1000αA1002αB≈=3α=3αB
From Eq. (iii) αA=3×9×10−6=27×10−6/∘C
from eq. (i) T=61000αA=6×1061000×27
=222.22∘C
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
_E01_013_Q01.png)
Knowledge Check
Find the temperature at which the fundamental frequency of an organ pipe is independent of small variation in temperature in terms of the coefficient of linear expansion ( α) of the material of the tube.
A1/3αB1/2αC1/4αD1/5αThe volume of a metal sphere increases by 0.24% when its temperature is raised by 40∘C . The coefficient of linear expansion of the metal is .......... .∘C
A2×105.∘C−1B6×10−5.∘C−1C18×10−5.∘C−1D1.2×10−5.∘C−1The volume of a block of a metal changes by 0.12% when it is heated through 20∘C . The coefficient of linear expansion of the metal is
A4×10−5∘C−1B2×10−5∘C−1C0.5×10−5∘C−1D4×10−4∘C−1
The radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ΔT so that its new temperature is T+ΔT. The increase in the volume of the sphere is approximately
View SolutionThe coefficient of linear expansion of a metal rod does not depend uponthe original length of the rod
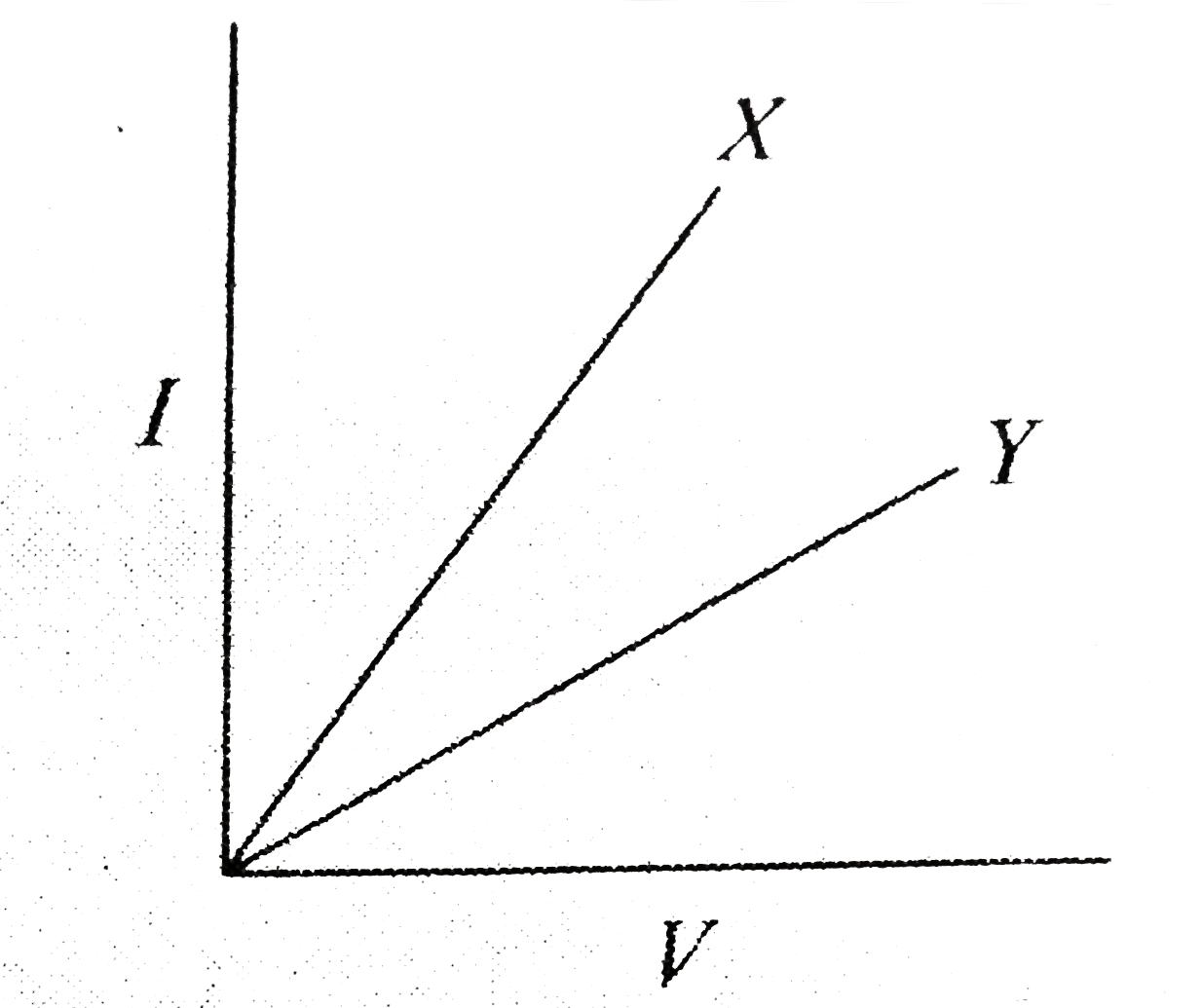
View SolutionThe voltage-current variations of two metallic wire X and Y at constant temperature is shown in fig Assumign that the wires have the same length and the same diameter, explain which of the two wires will have larger resisitivity.
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remian constant at any temperature then
View SolutionThe radius of metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature T, so that new temperature is T+ΔT. The increase in volume of sphere is approximately
View Solution