The length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remian constant at any temperature then
LA/LB=αA/αB
LA/LB=αB/αA
αA=αB
αAαB=1
The correct Answer is:B
To solve the problem, we need to analyze the condition under which the difference in lengths of the two metallic rods remains constant as the temperature changes. Let's denote the lengths of the rods at temperature θ as LA and LB, and their linear coefficients of expansion as αA and αB respectively.
1. Understanding Linear Expansion:
The change in length of a rod due to temperature change can be expressed as:
ΔL=α⋅L0⋅ΔT
where ΔL is the change in length, α is the linear coefficient of expansion, L0 is the original length, and ΔT is the change in temperature.
2. Change in Lengths of Rods:
For rod A, the change in length when the temperature changes by ΔT is:
ΔLA=αA⋅LA⋅ΔT
For rod B, the change in length is:
ΔLB=αB⋅LB⋅ΔT
3. Setting Up the Condition:
We want the difference in lengths LA−LB to remain constant. Therefore, the change in lengths must satisfy:
ΔLA−ΔLB=0
This implies:
αA⋅LA⋅ΔT=αB⋅LB⋅ΔT
4. Cancelling ΔT:
Since ΔT is common in both terms and is not zero, we can cancel it out:
αA⋅LA=αB⋅LB
5. Rearranging the Equation:
Rearranging the equation gives us:
LALB=αBαA
Conclusion:
Thus, the relationship that must hold for the difference in lengths to remain constant at any temperature is:
LALB=αBαA
The change in length of a rod due to temperature change can be expressed as:
ΔL=α⋅L0⋅ΔT
where ΔL is the change in length, α is the linear coefficient of expansion, L0 is the original length, and ΔT is the change in temperature.
For rod A, the change in length when the temperature changes by ΔT is:
ΔLA=αA⋅LA⋅ΔT
For rod B, the change in length is:
ΔLB=αB⋅LB⋅ΔT
We want the difference in lengths LA−LB to remain constant. Therefore, the change in lengths must satisfy:
ΔLA−ΔLB=0
This implies:
αA⋅LA⋅ΔT=αB⋅LB⋅ΔT
Since ΔT is common in both terms and is not zero, we can cancel it out:
αA⋅LA=αB⋅LB
Rearranging the equation gives us:
LALB=αBαA
Thus, the relationship that must hold for the difference in lengths to remain constant at any temperature is:
LALB=αBαA
Topper's Solved these Questions
Similar Questions
Two rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
View SolutionSTATEMENT - 1 : A metallic rod placed upon smooth surface is heated. The strain produced is ZERO.
STATEMENT - 2 : Strain is non-zero only when stress is developed in the rod.
STATEMENT - 3 : Two metallic rods of length l1 and l2 and coefficient of linear expansion α1 and α2 are heated such that the difference of their length ramains same at ALL termperatures Then α1α2=l2l1
View SolutionThere are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionTwo rods of lengths l1andl2 are made of materials having coefficients of linear expansion α1andα2 respectively. What could be the relation between above values, if the difference in the lengths of the two rods does not depends on temperature variation?
View SolutionTwo metallic rods of length l and 3l have coefficient of linear expansion α and 3α respectively. The coefficient of linear expansion ofr their series combinations, is
View SolutionCoefficient of linear expnsion of material of resistor is α . Its temperature coefficient of resistivity and resistance are αp and αR respectively , the correct relation is .
View SolutionTwo rods having length l1 and l2, made of materials with the linear coefficient of expansion α1 and α2 were welded together. The equivalent coefficients of linear expansion for the obtained rod:-

View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View SolutionThree rods of equal of length are joined to from an equilateral triangle ABC. D is the midpoint of AB. The coefficient of linear expansion is α1 for AB and α2 for AC and BC . If the distance DC remains constant for small changes in temperature,

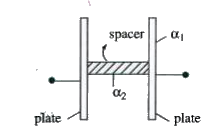
View SolutionA capacitor is to be designed to operate, with constant capacitance, even when temperature varies.The distance between plates is adjusted by spacer to compensate temperature effect. Let α1andα2 be the coefficient of thermal expansion of plate and spacer respectively. Find the ratio of α2α1 . So that no change in capacitance of capacitor with change in temperature.
View Solution

