A capacitor is to be designed to operate, with constant capacitance, even when temperature varies.The distance between plates is adjusted by spacer to compensate temperature effect. Let α1andα2 be the coefficient of thermal expansion of plate and spacer respectively. Find the ratio of α2α1 . So that no change in capacitance of capacitor with change in temperature.
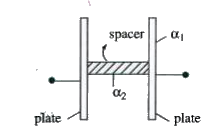
The correct Answer is:2
Step by step video & image solution for A capacitor is to be designed to operate, with constant capacitance, even when temperature varies.The distance between plates is adjusted by spacer to compensate temperature effect. Let alpha_(1) and alpha_(2) be the coefficient of thermal expansion of plate and spacer respectively. Find the ratio of alpha_2/alpha_1 . So that no change in capacitance of capacitor with change in temperature. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II LECTURE SHEET (ADVANCED))(Matrix Matching Type Questions)
1 Videos
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II LECTURE SHEET (ADVANCED))(Integer Type Questions )
3 Videos
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN)(Straight Objective Type Questions)
22 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
- COMMUNICATION SYSTEM BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)
20 Videos
Similar Questions
There are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionTwo conductors have the same resistance at 0∘C but their temperature coefficient of resistanc are α1andα2. The respective temperature coefficients of their series and parallel combinations are nearly
View SolutionA parallel plate capacitor of area A and separation d is provided with thin insulating spacers to keep its plates aligned in an environment of fluctuating temperature. If the coefficient of thermal expansion of material of the plate is α, find the coefficient of thernal expansion (αs) of the spacers in order that the capacitance does not vary with temperature. (Ignore effect of the spacers on capacitance.)
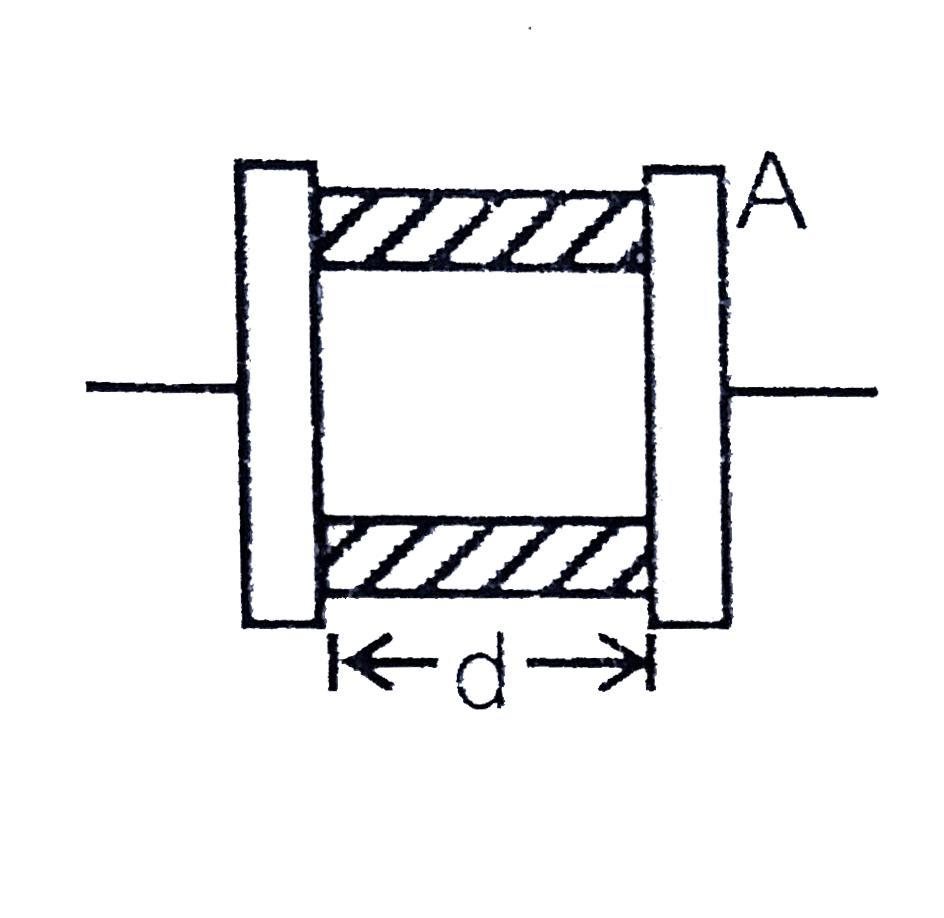
View SolutionTwo rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
View SolutionThe variation of volume V, with temperature T, keeping pressure constant is called the coefficient of thermal expansion (α) of a gas,
i.e., α=1V(δVδT)P.
For an ideal gas α is equal to
View SolutionTwo rods of lengths l1andl2 are made of materials having coefficients of linear expansion α1andα2 respectively. What could be the relation between above values, if the difference in the lengths of the two rods does not depends on temperature variation?
View SolutionShow that moment of inertia of a solid body of any shape changes with temperature as I=I0(1+2αθ). Where I0 is the moment of inertia at 0∘C and α is the coefficient of linear expansion of the solid.
View SolutionTwo different wires having lengths L1 and L2 and respective temperature coefficient of linear expansion α1 and α2 are joined end - to - end . Then the effective temperature coefficient of linear expansion is :
View SolutionTwo wires of resistance R1 and R2 have temperature coefficient of resistance α1 and α2 respectively. These are joined in series. The effective temperature coefficient of resistance is
View SolutionTwo wires of resistance R1 and R2 have temperature coefficient of resistance α1 and α2 respectively. These are joined in series. The effective temperature coefficient of resistance is
View Solution
