A uniform electric field in positive x-direction on exists in space. An uncharged solid conducting sphere is now placed in region of this uniform electric field. The centre of this sphere of radius R lies at origin. Then electric potential at any point on y−z plane (i.e. x=0 plane) due to only induced charged on surface of sphere.
will be positive
will be negative
will be zero
may be positive, zero or negative
The correct Answer is:C
To solve the problem, we need to analyze the situation where a uniform electric field is present, and an uncharged solid conducting sphere is placed in that field. The goal is to find the electric potential at any point on the y-z plane (where x=0) due to the induced charges on the surface of the sphere.
1. Understand the Setup:
- We have a uniform electric field directed in the positive x-direction.
- A solid conducting sphere of radius R is placed at the origin (0, 0, 0) of the coordinate system.
2. Induced Charges on the Sphere:
- When the conducting sphere is placed in the electric field, it will become polarized. The electric field will induce a positive charge on the hemisphere of the sphere that is facing the direction of the electric field (the right side, in this case) and a negative charge on the hemisphere that is facing away from the electric field (the left side).
- This results in a distribution of induced charges on the surface of the sphere.
3. Electric Potential Calculation:
- The electric potential at any point in space due to a charge distribution is given by the formula:
V=k∑qiri
where k is the Coulomb's constant, qi is the charge, and ri is the distance from the charge to the point where the potential is being calculated.
- However, in this case, we are interested in the potential at points on the y-z plane (where x=0) due to the induced charges.
4. Symmetry Argument:
- For any point on the y-z plane, there will be a corresponding point on the opposite side of the sphere that will have an equal and opposite charge.
- The potential due to the positive charge on the right hemisphere will be canceled out by the potential due to the negative charge on the left hemisphere at any point on the y-z plane.
5. Conclusion:
- Since the contributions to the potential from the positive and negative charges cancel each other out at every point on the y-z plane, the net electric potential at any point on the y-z plane due to the induced charges on the surface of the sphere is zero.
Thus, the electric potential at any point on the y-z plane due to the induced charges on the surface of the sphere is:
Electric Potential=0
- We have a uniform electric field directed in the positive x-direction.
- A solid conducting sphere of radius R is placed at the origin (0, 0, 0) of the coordinate system.
- When the conducting sphere is placed in the electric field, it will become polarized. The electric field will induce a positive charge on the hemisphere of the sphere that is facing the direction of the electric field (the right side, in this case) and a negative charge on the hemisphere that is facing away from the electric field (the left side).
- This results in a distribution of induced charges on the surface of the sphere.
- The electric potential at any point in space due to a charge distribution is given by the formula:
V=k∑qiri
where k is the Coulomb's constant, qi is the charge, and ri is the distance from the charge to the point where the potential is being calculated.
- However, in this case, we are interested in the potential at points on the y-z plane (where x=0) due to the induced charges.
- For any point on the y-z plane, there will be a corresponding point on the opposite side of the sphere that will have an equal and opposite charge.
- The potential due to the positive charge on the right hemisphere will be canceled out by the potential due to the negative charge on the left hemisphere at any point on the y-z plane.
- Since the contributions to the potential from the positive and negative charges cancel each other out at every point on the y-z plane, the net electric potential at any point on the y-z plane due to the induced charges on the surface of the sphere is zero.
Electric Potential=0
Topper's Solved these Questions
Similar Questions
A hollow insulated conducting sphere is given a positive charge of 10μC . What will be the electric field at the centre of the sphere it is radius is 2 metres ?
View SolutionA metallic solid sphere is placed in a uniform electric field. The lines of force follow the path(s) shown in Figure as
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionA solid metallic sphere is placed in a uniform electric field. Which of the lines A, B, C and D shows the correct path and why ?
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionA point positive charge is brought near an isolated conducting sphere as shown in figure the electric field is best given by
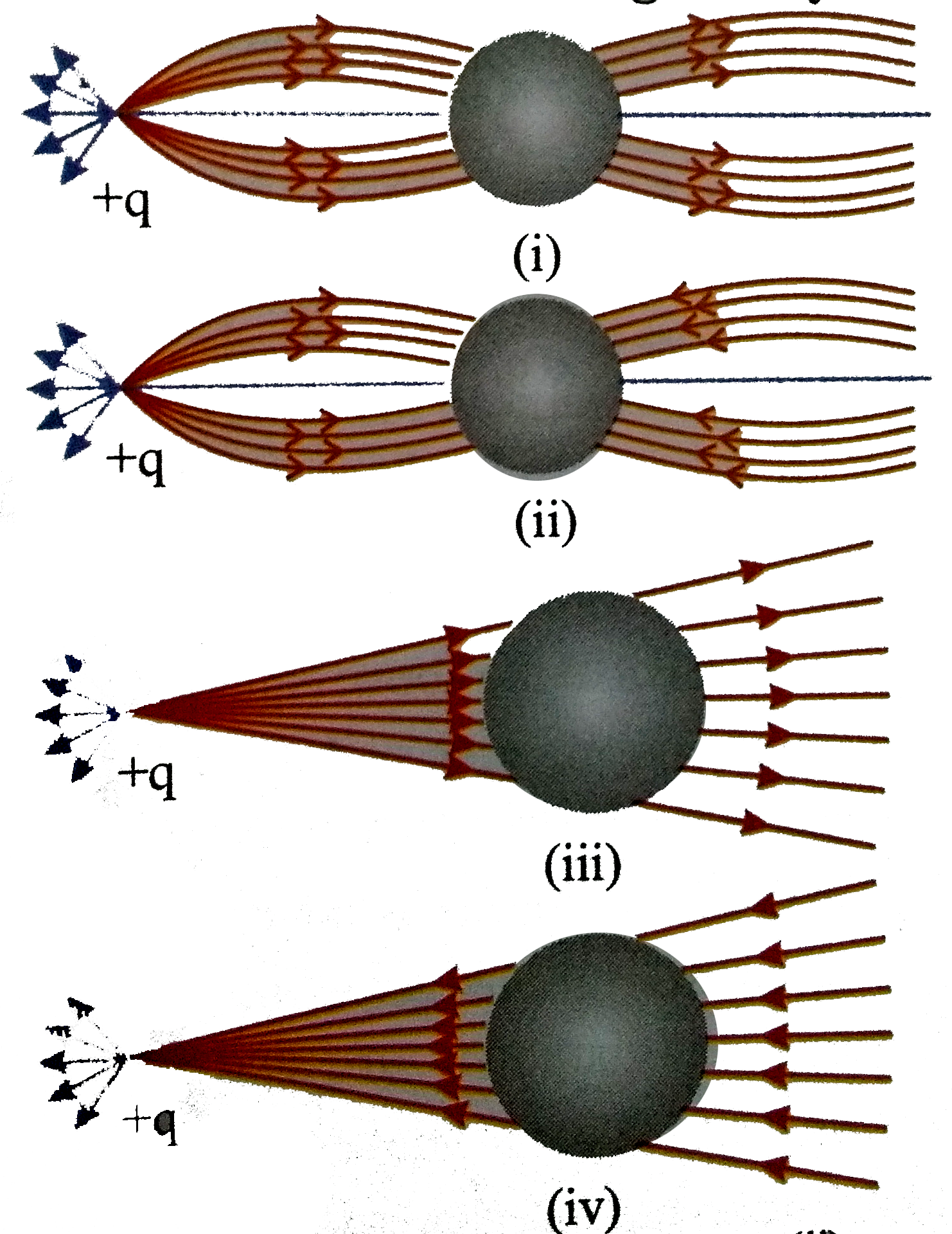
View SolutionA point positive charge is brought near an isolated conducting sphere. The electric field is best given by

View SolutionA point positive charge is brought near an isolated conducting sphere as shown in figure the electric field is best given by

View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution
