Two Aluminium rods and a steel rod of equal cross-sectional area and equal length are joined rigidly side by side as shown in figure. Initially the rods are at . Find the length of the rod at the temperature if young's modulus of elasticity of the aluminium and steel are and respectively and coefficient of linear expansion of aluminum and steel are and respectively.
The correct Answer is:

If rods are free to expand.
for steel (compression)
by solving (i) and (ii)
we get
then
Topper's Solved these Questions
Similar Questions
Two steel rods and an aluminium rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 00C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αaandαs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
steel
Aluminium
Steel

View SolutionTwo same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
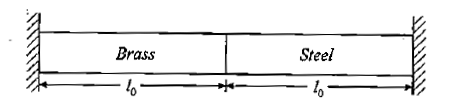
View Solution
Knowledge Check
Two rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
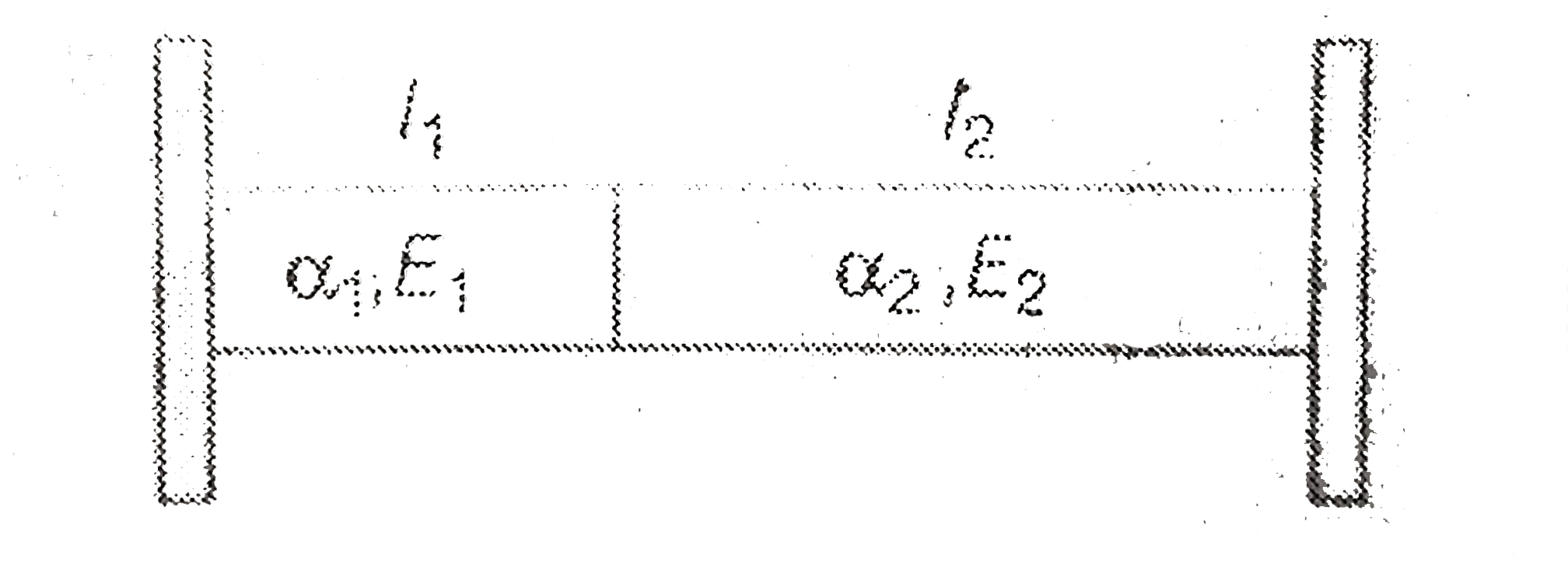 Athe strain produced in both rods is equalBthe stress produced in both the rods is equalCthe force exerted by one rod on the other is α1l1+α2l2l1E1+l2E2AtDthe force exerted by one rod on the other is (E1−E2)2AE1+E2
Athe strain produced in both rods is equalBthe stress produced in both the rods is equalCthe force exerted by one rod on the other is α1l1+α2l2l1E1+l2E2AtDthe force exerted by one rod on the other is (E1−E2)2AE1+E2A thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
AL0[1+α(θ1+θ2)]BL0(1+α(θ1+θ22))CL0(1+αθ1)DL0(1+α(θ1+θ22))A uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
A12ρgLB14ρgLCρgLDNone of these
What should be the sum of lengths of an aluminium and steel rod at 0∘C is, so that all the temperature their difference in length is 0.25m. (Take coefficient of linear expansion for aluminium and steel at 0∘C as 22×10−6/.∘C and 11×10−5/.∘C respectively.)
View SolutionThe length of two metallic rods at temperatures θ are LA and LB and their linear coefficient of expansion are αA and αB respectively. If the difference in their lengths is to remain constant at any temperature then
View SolutionTwo rods of different materials and identical cross sectional area, are joined face to face at one end their free ends are fixed to the rigid walls. If the temperature of the surroundings is increased by 30∘C, the magnitude of the displacement of the joint of the rod is (length of rods l1=l2=1unit, ratio of their young's moduli, Y1/Y2=2, coefficients of linear expansion are α1 and α2)
View SolutionA copper rod and a steel rod of equal cross -sections and lengths (L) are joined side by side and connected between two heat baths as shown in the figure. If heat flows through them from x=0 to x=2L at a steady rate, and conductivities of the metals are Kcu & Ksteel(Kcu>Ksteel), then the temperature varies with x as (convention and radiation are negligible)
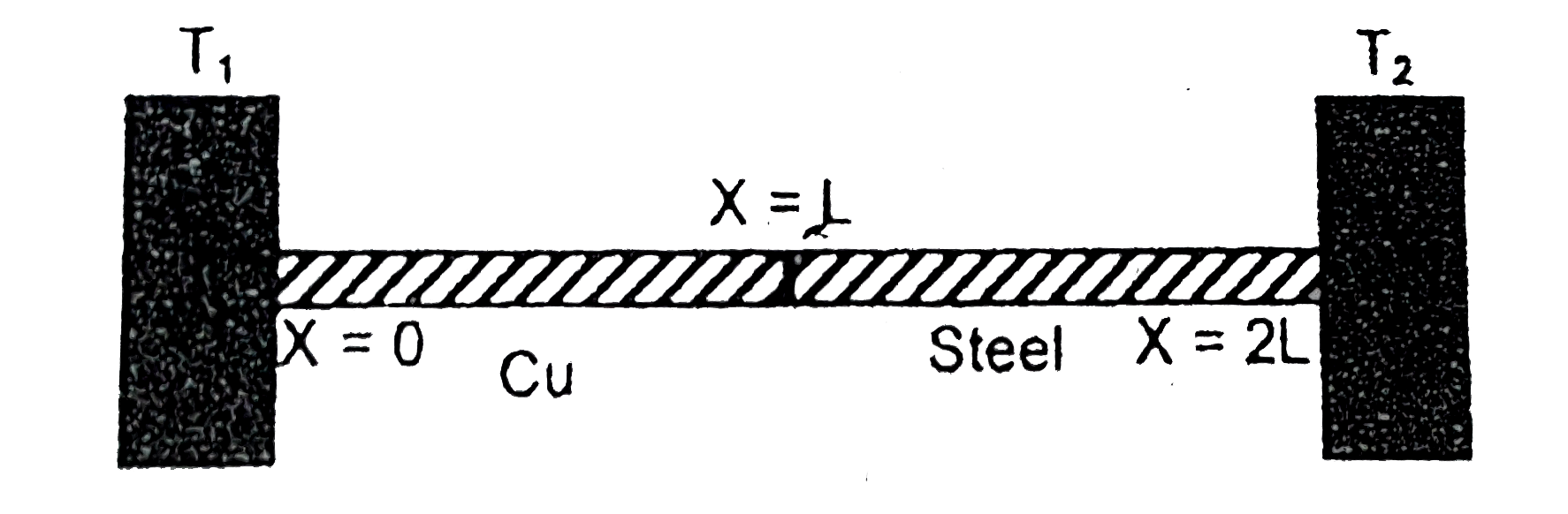
View SolutionA thin rod of negligible mass and area of cross section S is suspended vertically from one end. Length of the rod is L0 at T∘C . A mass m is attached to the lower end of the rod so that when temperature of the rod is reduced to 0∘C its length remains L0 Y is the Young’s modulus of the rod and α is coefficient of linear expansion of rod. Value of m is :
View Solution

