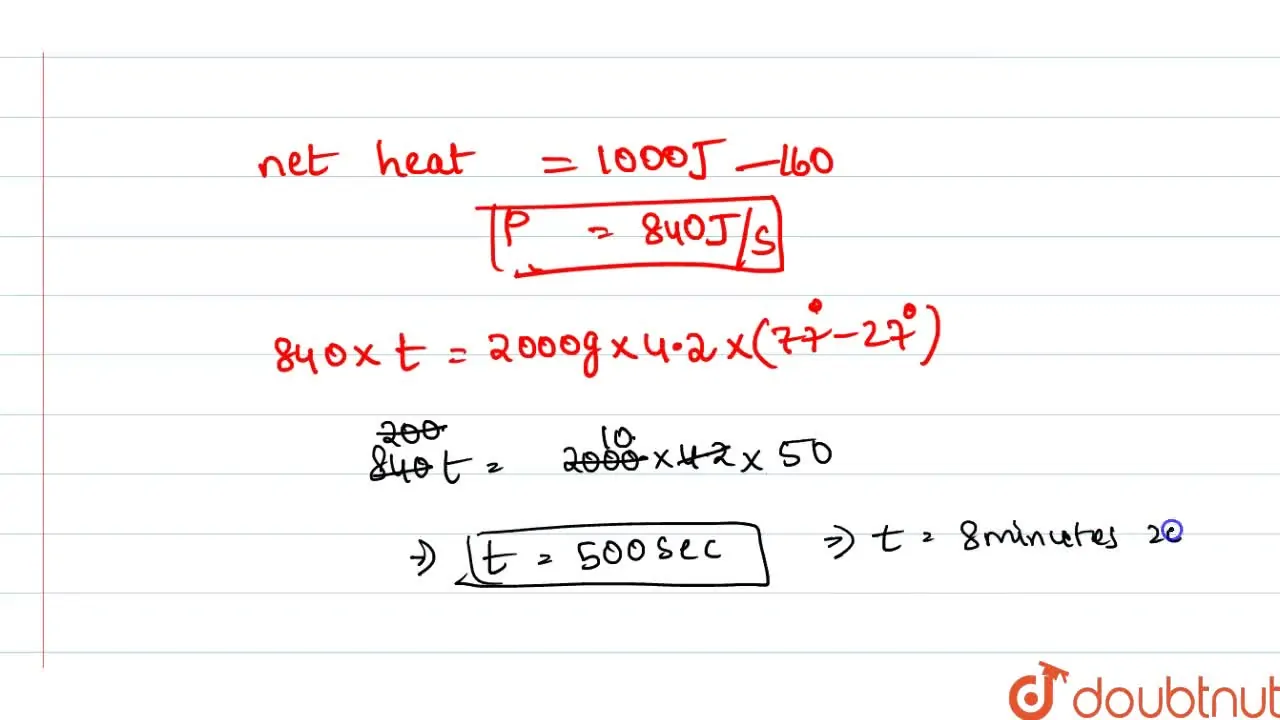litres water at is heated by a heater in an open container. On an average heat is lost to surroundings at the rate . The time required for the temperature to reach is
The correct Answer is:A
Net heat given/sec
if it taken time t then
.
Related Playlists
- BOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Advanced Level Problems13videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercie-31videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCECHAPTER - CALORIMETRYEXERCISE - Exercise19videos
CALORIMETRY
- BOOK - RESONANCECHAPTER - CAPACITOREXERCISE - Exercise45videos
CAPACITOR
Similar Questions
A kettle with 2 litre water at 27∘C is heated by operating coil heater of power 1 kW. The heat is lost to the atmosphere at constant rate 160J/s, when its lid is open. In how much time will water heated to 77∘C with the lid open ? (specific heat of water = 4.2kJ/∘C−kg)
View SolutionHeat required to increases the temperature of 1kg water by 20∘C
View SolutionHeat required to raise the temperature of one gram of water through 1∘C is
View SolutionTwo litres of water kept in a container at 27∘C is heated with a coil of 1 kW. The lid of the container is open and energy dissipates at the rate of 160 J/s. If the specific heat of water is 4.2 kJ/kg, then time taken by coil to raise the temperature of water from 27∘C to 77∘C is
View SolutionWater of volume 2 litre in a container is heated with a coil of 1kWat27∘C. The lid of the container is open and energy dissipates at rate of 160J/s. In how much time temperature will rise from 27∘C→77∘C Given specific heat of water is
[4.2kJ/kg]View SolutionWater of volume 2 liter in a container is heated with a coil of 1 kW at 27∘C. The lid of the container is open and energy dissipates at the rate of 160Js−1 . In how much time, temperature will rise from 27∘Cto77∘C ?
View SolutionWater of volume 2 litre in a container is heated with a coil of 1kWat27∘C. The lid of the container is open and energy dissipates at rate of 160J/s. In how much time temperature will rise from 27∘C→77∘C [Given specific heat of water is
4.2kJ/kg]View SolutionWater of volume 4L in a closed container is heated with a coil of 2 kW. While water is heated, the container loses energy at a rate of 120 J/s. In how much time will the temperature of water rise from 27∘C to 77∘C? (Specific heat of water is 4.2 kJ/kg and that of the container is negligible).
View SolutionWater of volume 2 liter in a container is heated with a coil of 1kW at 27∘C. The lid of the container is open and energy dissipates at rate of 160Js. In how much time (in s ) temperature will rise from 27∘C to 77∘C? (Given: Specific heat of water is 4.2kJkg)
View SolutionIn a container of negligible heat capacity, 200 g ice at 0∘C and 100 g steam at 0∘C are added to 200 g of water that has temperature 55∘C Assume no heat is lost to the surroundings and the pressure in the container is constant 1.0 atm.
At the final temperature, mass of the total water present in the system, isView Solution