Two coherent fight sources A and B with separation 2λ are placed on the x-axis symme-trically about the origion. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and with centre at the origion.
To solve the problem of finding the positions of maxima on a circle of large radius in the x-y plane due to two coherent light sources A and B, we can follow these steps:
Step 1: Understand the Setup
We have two coherent light sources A and B separated by a distance of 2λ along the x-axis, which means:
- Source A is located at (−λ,0)
- Source B is located at (λ,0)
Step 2: Condition for Maxima
For constructive interference (maxima) to occur at any point P on the circle, the path difference between the light waves coming from sources A and B must be an integer multiple of the wavelength λ:
dcosθ=nλ
where d is the distance between the two sources, θ is the angle made with the x-axis, and n is an integer (0, ±1, ±2, ...).
Step 3: Substitute the Values
Since d=2λ, we can rewrite the condition for maxima as:
2λcosθ=nλ
Dividing both sides by λ (assuming λ≠0):
2cosθ=n
This gives us:
cosθ=n2
Step 4: Determine Possible Values of n
The cosine function has a range of (−1,1). Therefore, for cosθ=n2 to be valid:
−1≤n2≤1
This implies:
−2≤n≤2
Thus, the possible integer values for n are −2,−1,0,1,2.
Step 5: Calculate Corresponding Angles
Now we can find the angles θ for each value of n:
- For n=−2:
cosθ=−1⇒θ=180∘
- For n=−1:
cosθ=−0.5⇒θ=120∘,240∘
- For n=0:
cosθ=0⇒θ=90∘,270∘
- For n=1:
cosθ=0.5⇒θ=60∘,300∘
- For n=2:
cosθ=1⇒θ=0∘
Step 6: List All Maxima Positions
The angles corresponding to maxima are:
- 0∘
- 60∘
- 90∘
- 120∘
- 180∘
- 240∘
- 270∘
- 300∘
Step 7: Convert Angles to Cartesian Coordinates
For a circle of radius R, the positions of maxima can be expressed in Cartesian coordinates as:
- (Rcosθ,Rsinθ)
Final Positions of Maxima
The positions of maxima on the circle are:
1. (R,0) at 0∘
2. (R⋅12,R⋅√32) at 60∘
3. (0,R) at 90∘
4. (−R⋅12,R⋅√32) at 120∘
5. (−R,0) at 180∘
6. (−R⋅12,−R⋅√32) at 240∘
7. (0,−R) at 270∘
8. (R⋅12,−R⋅√32) at 300∘
We have two coherent light sources A and B separated by a distance of 2λ along the x-axis, which means:
- Source A is located at (−λ,0)
- Source B is located at (λ,0)
For constructive interference (maxima) to occur at any point P on the circle, the path difference between the light waves coming from sources A and B must be an integer multiple of the wavelength λ:
dcosθ=nλ
where d is the distance between the two sources, θ is the angle made with the x-axis, and n is an integer (0, ±1, ±2, ...).
Since d=2λ, we can rewrite the condition for maxima as:
2λcosθ=nλ
Dividing both sides by λ (assuming λ≠0):
2cosθ=n
This gives us:
cosθ=n2
The cosine function has a range of (−1,1). Therefore, for cosθ=n2 to be valid:
−1≤n2≤1
This implies:
−2≤n≤2
Thus, the possible integer values for n are −2,−1,0,1,2.
Now we can find the angles θ for each value of n:
- For n=−2:
cosθ=−1⇒θ=180∘
- For n=−1:
cosθ=−0.5⇒θ=120∘,240∘
- For n=0:
cosθ=0⇒θ=90∘,270∘
- For n=1:
cosθ=0.5⇒θ=60∘,300∘
- For n=2:
cosθ=1⇒θ=0∘
The angles corresponding to maxima are:
- 0∘
- 60∘
- 90∘
- 120∘
- 180∘
- 240∘
- 270∘
- 300∘
For a circle of radius R, the positions of maxima can be expressed in Cartesian coordinates as:
- (Rcosθ,Rsinθ)
The positions of maxima on the circle are:
1. (R,0) at 0∘
2. (R⋅12,R⋅√32) at 60∘
3. (0,R) at 90∘
4. (−R⋅12,R⋅√32) at 120∘
5. (−R,0) at 180∘
6. (−R⋅12,−R⋅√32) at 240∘
7. (0,−R) at 270∘
8. (R⋅12,−R⋅√32) at 300∘
Topper's Solved these Questions
Similar Questions
_E01_036_Q01.png)
Two point source separated by d=5μm emit light of wavelength λ=2μm in phase A cicular wire of radius 20μm is placed aournd the source as shown in figure.
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=5λ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
View SolutionA point charge q is placed at origin. Find the flux of electric,produced due to this charge, through a circle of radius R lying in y-z plane. The centre of the circle lies at (x,0).
View SolutionTwo coherent sources emit light of wavelength λ. Separation between them, d=4λ.
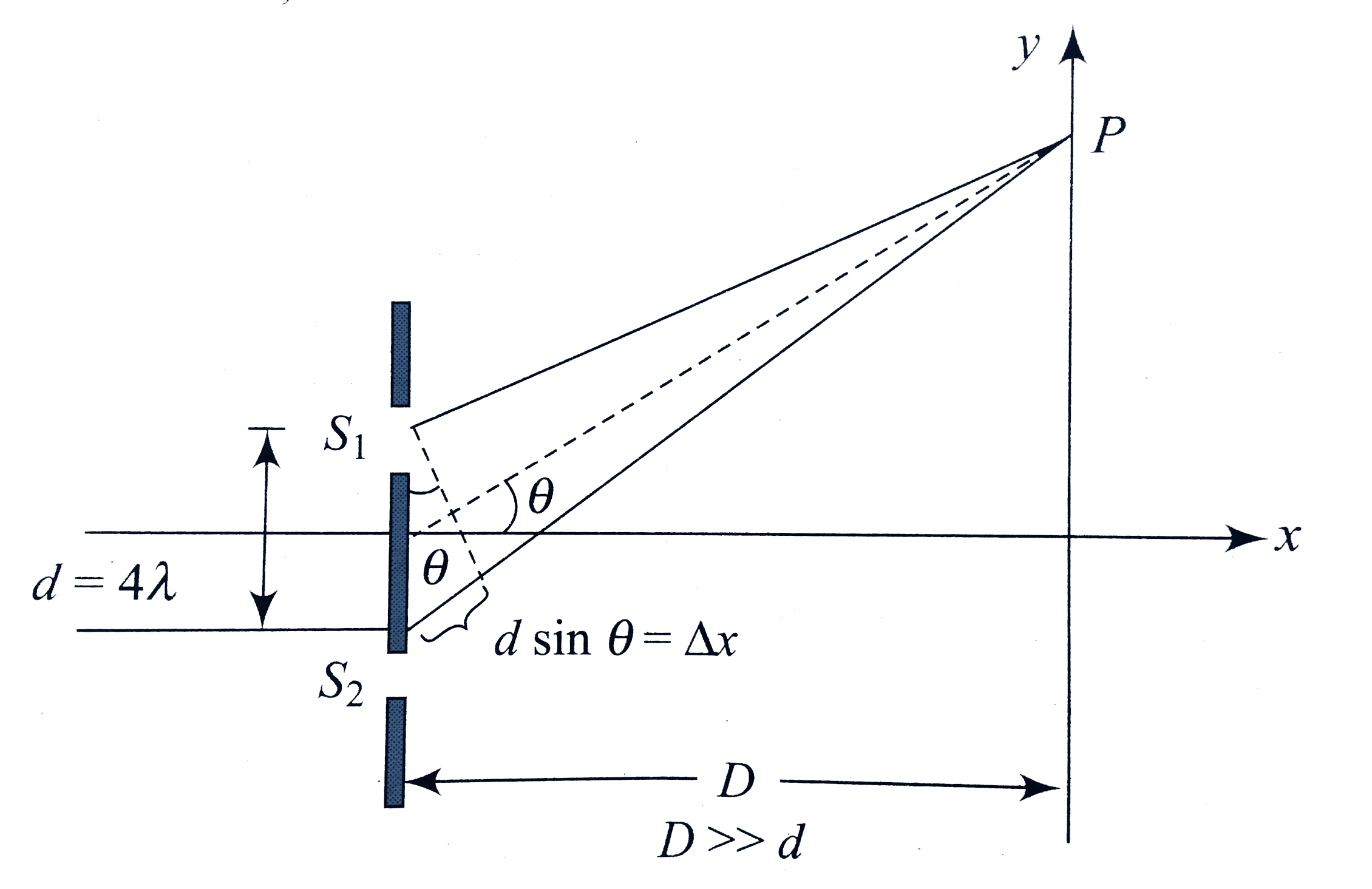
If a detector moves along the y-axis, what is the maximum number of minima observed?
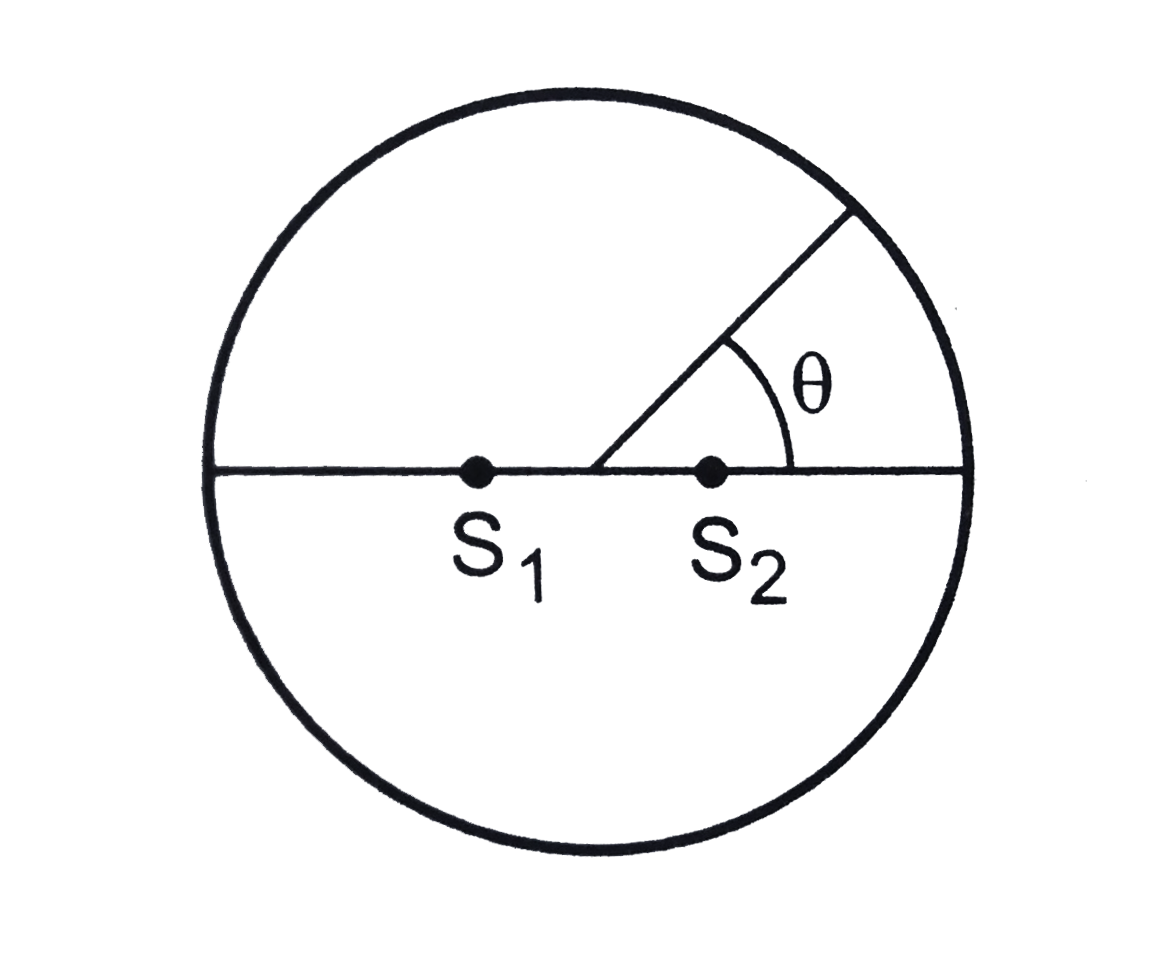
View SolutionFigure shows two coherent sources S1andS2which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire at large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2, is at the centre of the wire. Find the angular positions 0 on the wire for which constructive interference takes place.
View SolutionAssertion: Distance between two coherent sources S1andS2 is 4λ. A large circle is drawn around these sources with centre of circle lying at centre of S1andS2. There are total 16 maxima on this circle.
Reason: Total number of minimas on this circle are less, compared to total number of maximas.
View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionFour monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
View Solution
