Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
20
22
24
26
The correct Answer is:a
To solve the problem, we will analyze the situation step by step.
Step 1: Understand the Configuration
We have two coherent sources S1 and S2 placed on a diameter of a circle of radius R with a separation x (where x≪R). The sources emit waves of identical wavelength λ.
Hint: Visualize the setup by sketching the circle and marking the positions of the two sources.
Step 2: Determine the Path Difference
The path difference Δx between the waves from the two sources at any point on the circle is given by the formula:
Δx=S1P−S2P
where P is any point on the circumference of the circle. For constructive interference (maxima), the path difference must be an integer multiple of the wavelength:
Δx=nλ
where n is an integer (0, 1, 2, ...).
Hint: Remember that maxima occur when the path difference is a multiple of the wavelength.
Step 3: Calculate Maximum Points
Given that the separation x=5λ, we can find the number of maxima on the circle. The maximum path difference between the two sources occurs at points on the circle directly opposite each other, which is equal to the separation x.
The maximum path difference that can occur on the circle is x. Since x=5λ, we can have:
Δx=0,λ,2λ,3λ,4λ,5λ
This means that there are 6 values of n (from 0 to 5) for which maxima can occur.
Hint: Count the number of integer values of n from 0 to the maximum path difference divided by λ.
Step 4: Symmetry of the Circle
Due to the symmetry of the arrangement, for each maximum on one side of the center, there is an equivalent maximum on the other side. Therefore, for each n from 1 to 5, there are two maxima (one on each side of the center).
Hint: Consider how symmetry affects the number of maxima on both sides of the center.
Step 5: Total Count of Maxima
Including the central maximum (where n=0), we have:
- 1 maximum at n=0
- 5 maxima from n=1 to n=5, each contributing 2 maxima due to symmetry.
Thus, the total number of maxima is:
1+5×2=1+10=11
Hint: Make sure to include the central maximum when counting.
Final Answer
The total number of points on the circle of maximum intensity is 11.
We have two coherent sources S1 and S2 placed on a diameter of a circle of radius R with a separation x (where x≪R). The sources emit waves of identical wavelength λ.
The path difference Δx between the waves from the two sources at any point on the circle is given by the formula:
Δx=S1P−S2P
where P is any point on the circumference of the circle. For constructive interference (maxima), the path difference must be an integer multiple of the wavelength:
Δx=nλ
where n is an integer (0, 1, 2, ...).
Given that the separation x=5λ, we can find the number of maxima on the circle. The maximum path difference between the two sources occurs at points on the circle directly opposite each other, which is equal to the separation x.
Δx=0,λ,2λ,3λ,4λ,5λ
This means that there are 6 values of n (from 0 to 5) for which maxima can occur.
Due to the symmetry of the arrangement, for each maximum on one side of the center, there is an equivalent maximum on the other side. Therefore, for each n from 1 to 5, there are two maxima (one on each side of the center).
Including the central maximum (where n=0), we have:
- 1 maximum at n=0
- 5 maxima from n=1 to n=5, each contributing 2 maxima due to symmetry.
1+5×2=1+10=11
The total number of points on the circle of maximum intensity is 11.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
Two identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=5λ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
View SolutionTwo sources of sound are placed along the diameter of a circle of radius R(R>>41). How many minima will be heard as one moves along the perimeter of circle.
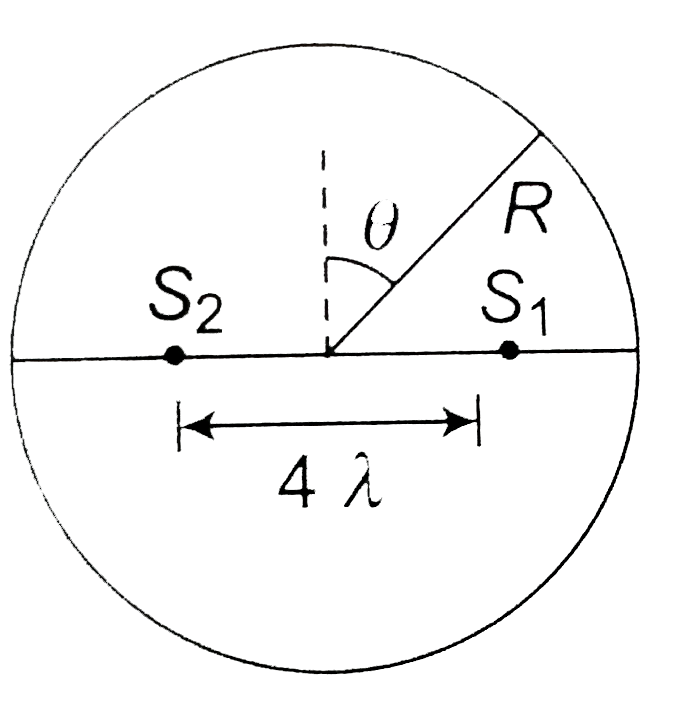
View Solution
Knowledge Check
The equation of two diameters of a cirlce are x−y=5 and 2x+y=4 and the radius of the circle is 5 units, then the equation of the circle is
Ax2+y2−6x+4y−12=0Bx2+y2+6x−4y−12=0Cx2+y2+6x+4y+12=0Dx2+y2−6x+4y+12=0
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionTwo coherent fight sources A and B with separation 2λ are placed on the x-axis symme-trically about the origion. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and with centre at the origion.
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionIf the equations of the two diameters of a circle are x−y=5 and 2x+y=4 and the radius of the circle is 5, find the equation of the circle.
View SolutionTwo coherent sources separated by distance d are radiating in phase having wavelength λ. A detector moves in a big circle around the two sources in the plane of the two sources. The angular position of n=4 interference maxima is given as

View SolutionThree dipoles each of dipole moment of magnitude p are placed tangentially on a circle of radius R in its plae positioned at equal angle from each other as shown in the figure. Then the magnitude of electric field intensity at the centre of the circle will be :
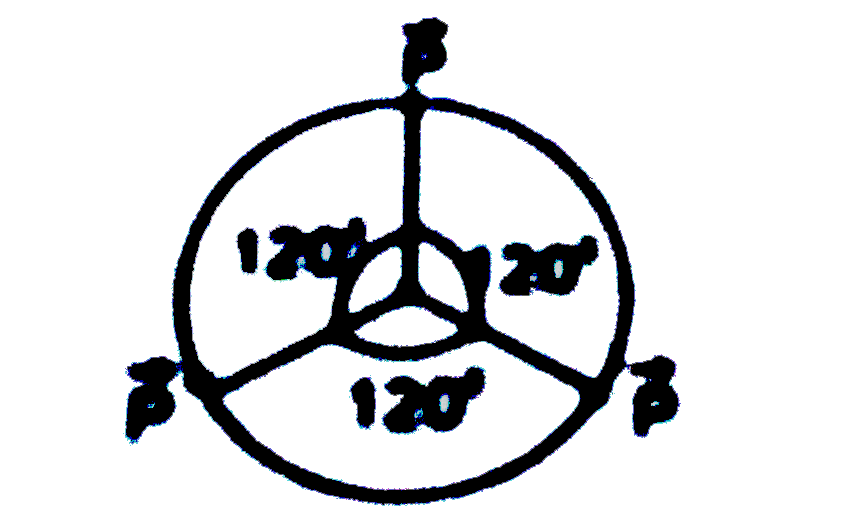
View Solution
