Light of wavelength λ=5890Å fall on a double-slit arrangement having separation d=0.2mm. A thin lens of focal length f=1m is placed near the slits. The linear separation of fringes on a screen placed in the focal plane of the lens is
3 mm
4 mm
2 mm
1 mm
The correct Answer is:a.
To solve the problem step by step, we will follow these calculations:
Step 1: Understand the given values
- Wavelength of light, λ=5890Å=5890×10−10m
- Separation of the slits, d=0.2mm=0.2×10−3m
- Focal length of the lens, f=1m
Step 2: Write the formula for fringe width
The formula for the fringe width β in a double-slit experiment with a lens is given by:
β=fλd
Step 3: Substitute the values into the formula
Now, we will substitute the values into the formula:
β=1m×5890×10−10m0.2×10−3m
Step 4: Calculate the numerator and denominator
Calculating the numerator:
1×5890×10−10=5890×10−10m
Calculating the denominator:
0.2×10−3=2×10−4m
Step 5: Perform the division
Now, we can perform the division:
β=5890×10−102×10−4=58902×10−10+4=2945×10−6m
Step 6: Convert to millimeters
To convert from meters to millimeters:
β=2945×10−6m=2.945mm≈3mm
Conclusion
The linear separation of fringes on the screen placed in the focal plane of the lens is approximately 3mm.
Final Answer
The correct option is 3mm.
---
- Wavelength of light, λ=5890Å=5890×10−10m
- Separation of the slits, d=0.2mm=0.2×10−3m
- Focal length of the lens, f=1m
The formula for the fringe width β in a double-slit experiment with a lens is given by:
β=fλd
Now, we will substitute the values into the formula:
β=1m×5890×10−10m0.2×10−3m
Calculating the numerator:
1×5890×10−10=5890×10−10m
0.2×10−3=2×10−4m
Now, we can perform the division:
β=5890×10−102×10−4=58902×10−10+4=2945×10−6m
To convert from meters to millimeters:
β=2945×10−6m=2.945mm≈3mm
The linear separation of fringes on the screen placed in the focal plane of the lens is approximately 3mm.
The correct option is 3mm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
Rays of light from Sunn falls on a biconvex lens of focal length f an the circular image of Sun of radius r is formed on the focal plane of the lens. Then,
View SolutionA source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
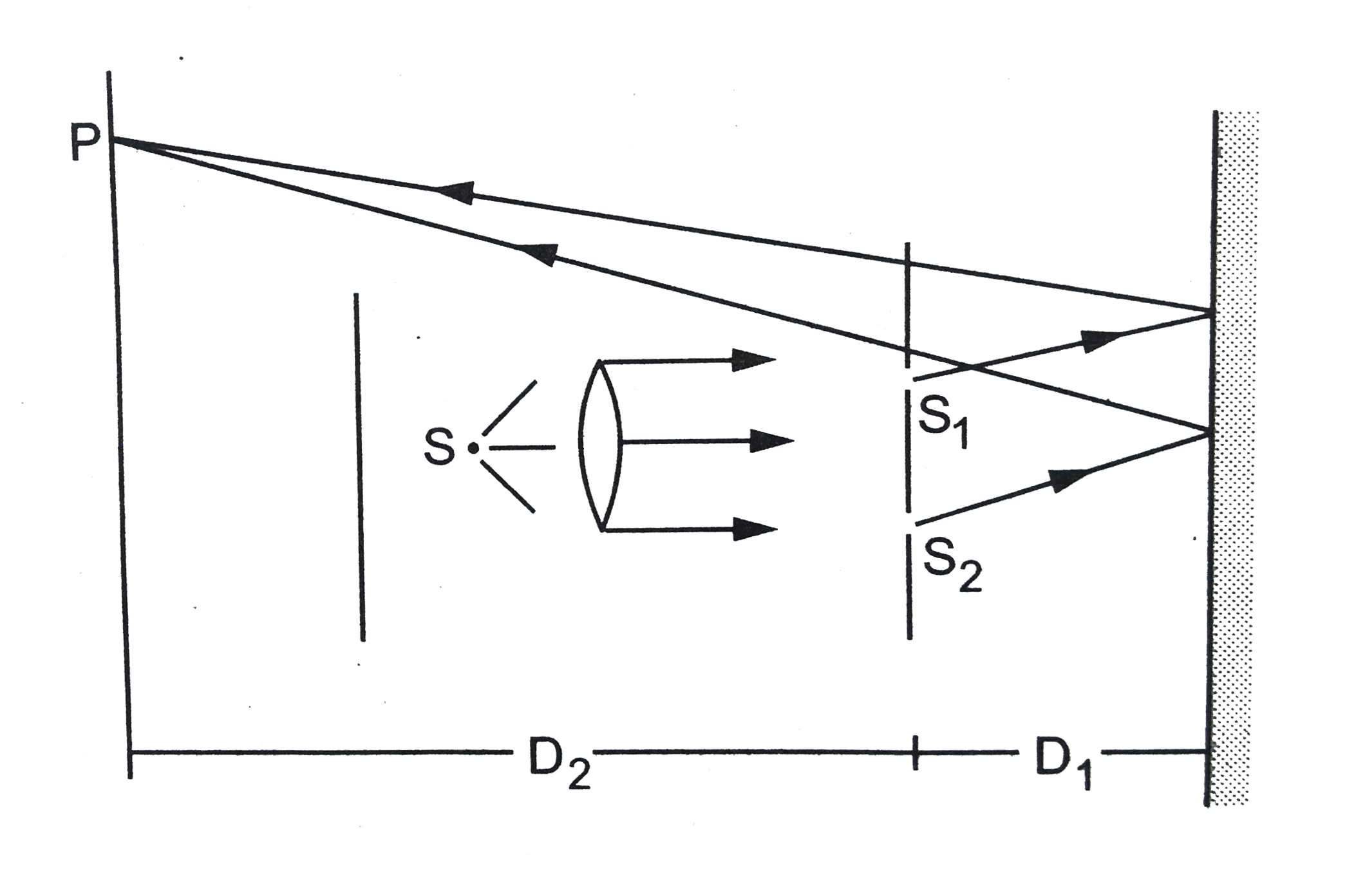
View SolutionA coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in figure
If the incient beam falls normally on the double-slit apparatus, find the order of the interference minima on the screen
View SolutionLights of wavelengths λ1=4500Å,λ2=6000Å are sent through a double slit arrangement simultaneously. Then
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
View SolutionThe distance between an electric lamp and a screen is d=1m. A convergent lens of focal length f=21cm is placed between the lamp and the lens such that a sharp image of the lamp filament is formed on the screen.
View SolutionLaser light of wavelength 630 nm is incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits, calculate :
fringe separation i.e., fringe width
View SolutionLight of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
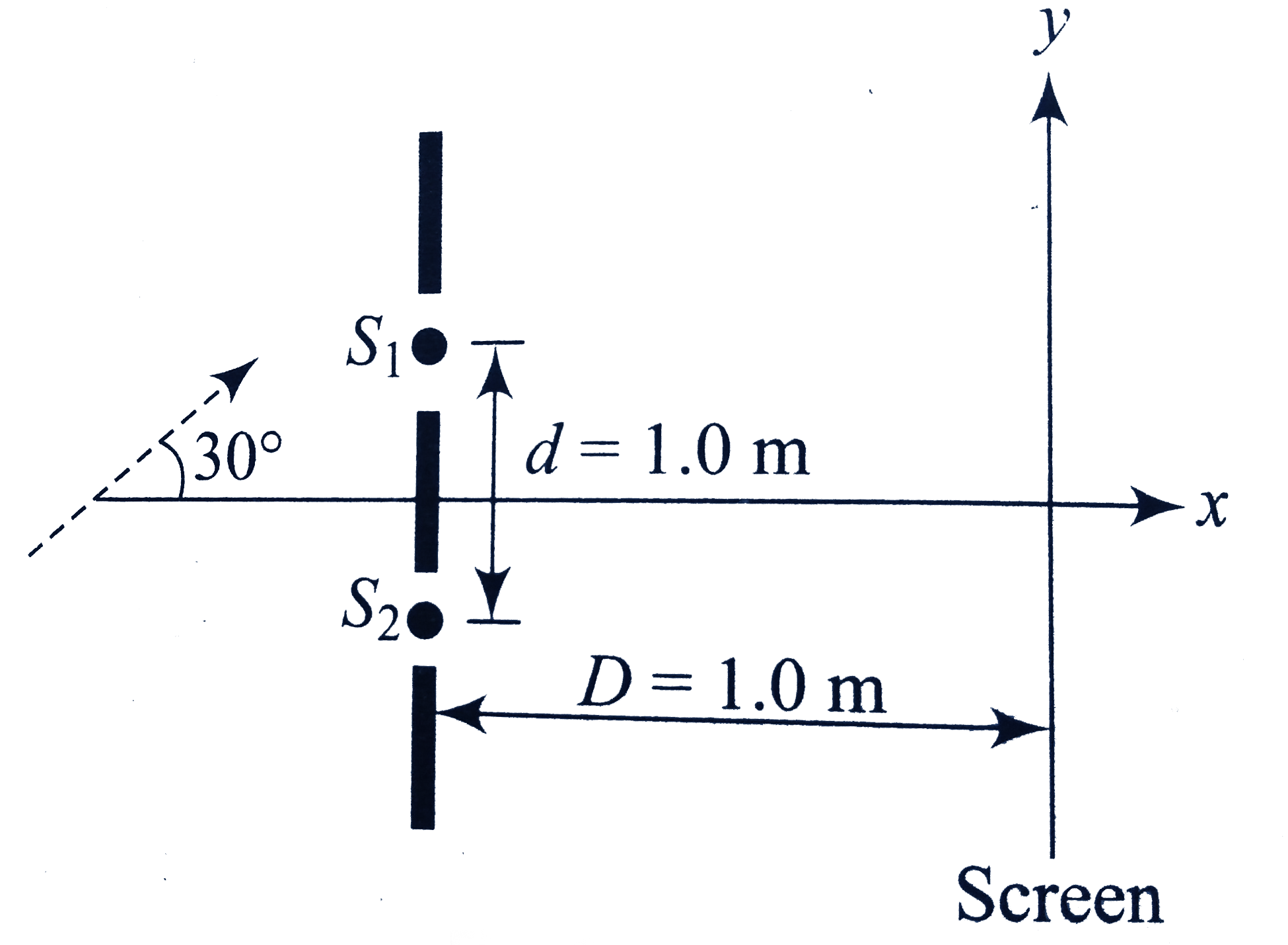
View SolutionIn a Young's double slit experiment, a parallel beam containing wavelengths λ1=4000Å and λ2=5600Å is incident at an angle ϕ=30∘ on a diaphragm having narrow slits at separation d=2mm. The screen is placed at a distance D =40 cm from the slits. a mica slab of thickness t=5mm is placed in front of one of the slits and whole of the apparatus is submerged in water. if the central bright fringe is observed at C, determine.

(i) The refractive index of the slab
(ii) The distance of first black line from C
both wavelength are in air. take μw=43
View SolutionIn Young's experiment, light of wavelength 600 nm falls on the double slits separated by 0.1 mm. What is the highest order of maximum intensity in the interference pattern obtained on a screen kept 3 m from the slits? How does the highest order change if the distance of screen from the slits is changed?
View Solution
