Consider a pendulum consisting of a massless string with a mass at one end. The mass is held with the string horizontal and then released. The mass swings down, and on its way back up, the string is cut at point P when it makes an angle of with θ the vertical. Find the angle for θ which horizontal range .R. is maximum.
To solve the problem of finding the angle θ for which the horizontal range R is maximum when the pendulum's string is cut, we can follow these steps:
1. Understanding the System:
The pendulum consists of a mass attached to a massless string. When the mass is released from the horizontal position, it swings down and gains speed due to gravitational potential energy converting into kinetic energy.
2. Applying Conservation of Energy:
When the pendulum is released from the horizontal position, its initial potential energy is converted into kinetic energy at the lowest point. The height h from which it falls can be expressed in terms of the length l of the string and the angle θ:
h=l(1−cosθ)
The potential energy at the top is:
PE=mgh=mg(l(1−cosθ))
At the lowest point, all potential energy converts to kinetic energy:
KE=12mv2
Setting PE=KE:
mg(l(1−cosθ))=12mv2
Canceling m and rearranging gives:
v2=2g(l(1−cosθ))
3. Finding the Velocity:
The velocity v of the mass when the string is cut at angle θ is:
v=√2g(l(1−cosθ))
4. Projectile Motion:
When the string is cut, the mass behaves like a projectile. The horizontal and vertical components of the velocity are:
Vx=vcosθ,Vy=vsinθ
5. Time of Flight:
The time of flight t until the mass hits the ground can be calculated using the vertical motion equation:
t=2Vyg=2(vsinθ)g
6. Horizontal Range:
The horizontal range R can be expressed as:
R=Vx⋅t=(vcosθ)⋅(2(vsinθ)g)
Substituting for v:
R=2v2sinθcosθg
Using v2=2g(l(1−cosθ)):
R=2(2g(l(1−cosθ)))sinθcosθg=4l(1−cosθ)sinθcosθ
7. Maximizing the Range:
To maximize R, we can use the identity sin(2θ)=2sinθcosθ:
R=2l(1−cosθ)sin(2θ)
Differentiate R with respect to θ and set the derivative to zero to find the maximum.
8. Setting up the Equation:
After differentiation and simplification, we arrive at:
cos3θ=2sin2θcosθ
Dividing by cosθ (assuming cosθ≠0):
cos2θ=2sin2θ
9. Using Trigonometric Identity:
Using sin2θ+cos2θ=1:
cos2θ=2(1−cos2θ)
Rearranging gives:
3cos2θ=2⟹cos2θ=23
10. Finding θ:
Thus, we find:
θ=tan−1(1√2)
Final Answer:
The angle θ for which the horizontal range R is maximum is:
θ=tan−1(1√2)
The pendulum consists of a mass attached to a massless string. When the mass is released from the horizontal position, it swings down and gains speed due to gravitational potential energy converting into kinetic energy.
When the pendulum is released from the horizontal position, its initial potential energy is converted into kinetic energy at the lowest point. The height h from which it falls can be expressed in terms of the length l of the string and the angle θ:
h=l(1−cosθ)
The potential energy at the top is:
PE=mgh=mg(l(1−cosθ))
At the lowest point, all potential energy converts to kinetic energy:
KE=12mv2
Setting PE=KE:
mg(l(1−cosθ))=12mv2
Canceling m and rearranging gives:
v2=2g(l(1−cosθ))
The velocity v of the mass when the string is cut at angle θ is:
v=√2g(l(1−cosθ))
When the string is cut, the mass behaves like a projectile. The horizontal and vertical components of the velocity are:
Vx=vcosθ,Vy=vsinθ
The time of flight t until the mass hits the ground can be calculated using the vertical motion equation:
t=2Vyg=2(vsinθ)g
The horizontal range R can be expressed as:
R=Vx⋅t=(vcosθ)⋅(2(vsinθ)g)
Substituting for v:
R=2v2sinθcosθg
Using v2=2g(l(1−cosθ)):
R=2(2g(l(1−cosθ)))sinθcosθg=4l(1−cosθ)sinθcosθ
To maximize R, we can use the identity sin(2θ)=2sinθcosθ:
R=2l(1−cosθ)sin(2θ)
Differentiate R with respect to θ and set the derivative to zero to find the maximum.
After differentiation and simplification, we arrive at:
cos3θ=2sin2θcosθ
Dividing by cosθ (assuming cosθ≠0):
cos2θ=2sin2θ
Using sin2θ+cos2θ=1:
cos2θ=2(1−cos2θ)
Rearranging gives:
3cos2θ=2⟹cos2θ=23
Thus, we find:
θ=tan−1(1√2)
The angle θ for which the horizontal range R is maximum is:
θ=tan−1(1√2)
Similar Questions
A simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionIn a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle thit θ with the vertical. Find the work done by the force F
 .
.
View SolutionOne end of ideal string tied up with fixed suppot & other end is tied with a bob. The string is released from horizontal position. When string makes an angle of θ with vertically downward direction then the acceleration vector of bob is horizontal then θ is
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. tension in the string
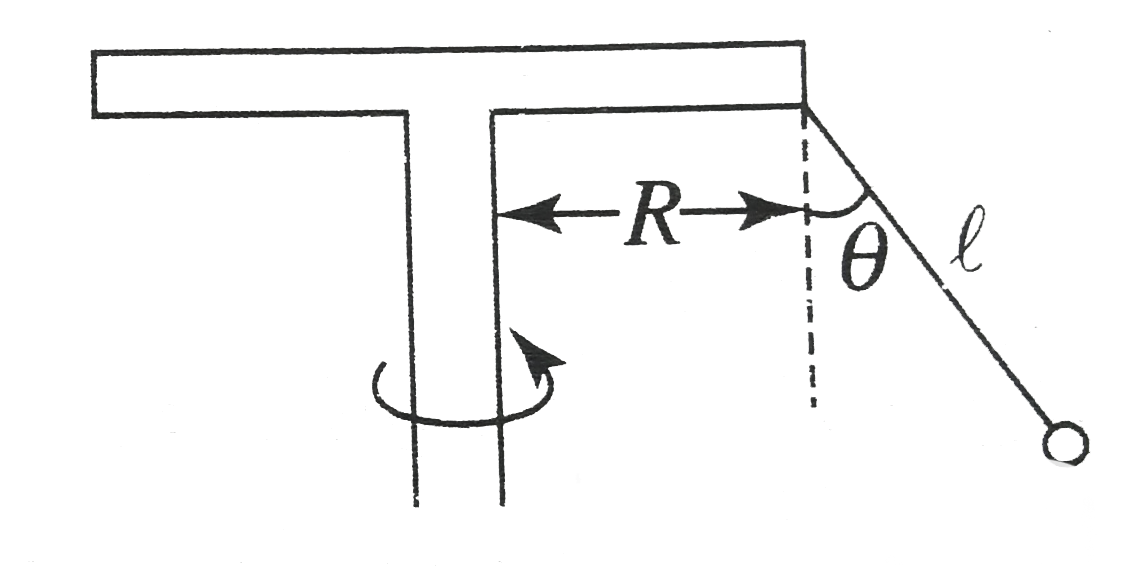
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA pendulum consisting of a small sphere of mass m, suspended by a inextensible and massless string of length 1 , is made to swing in a vertical plane. If the breaking strength of the string is 2 mg, then the maximum angular amplitude of the displacement from the vertical can be
View Solution
