A 2kg block is dropped from a height of 0.4 m on a spring of force constant 1960Nm−1. The maximum compression of the spring is
10cm
20cm
30cm
40cm
The correct Answer is:C
To solve the problem of finding the maximum compression of a spring when a 2 kg block is dropped from a height of 0.4 m onto it, we can follow these steps:
Step 1: Calculate the potential energy (PE) of the block at the height of 0.4 m.
The potential energy of the block when it is at height h is given by the formula:
PE=mgh
where:
- m=2kg (mass of the block)
- g=9.81m/s2 (acceleration due to gravity)
- h=0.4m (height from which the block is dropped)
Calculating:
PE=2kg×9.81m/s2×0.4m=7.848J
Step 2: Set the potential energy equal to the elastic potential energy (EPE) of the spring at maximum compression.
The elastic potential energy stored in the spring when compressed by a distance x is given by:
EPE=12kx2
where:
- k=1960N/m (spring constant)
- x is the maximum compression of the spring.
Setting the potential energy equal to the elastic potential energy:
mgh=12kx2
Substituting the values we have:
7.848J=12×1960N/m×x2
Step 3: Solve for x2.
Rearranging the equation:
x2=2×7.848J1960N/m
Calculating:
x2=15.6961960≈0.008m2
Step 4: Calculate x.
Taking the square root:
x=√0.008≈0.0894m
Step 5: Convert x to centimeters.
To convert meters to centimeters, multiply by 100:
x≈0.0894m×100≈8.94cm
Final Answer:
The maximum compression of the spring is approximately 8.94 cm.
---
The potential energy of the block when it is at height h is given by the formula:
PE=mgh
where:
- m=2kg (mass of the block)
- g=9.81m/s2 (acceleration due to gravity)
- h=0.4m (height from which the block is dropped)
PE=2kg×9.81m/s2×0.4m=7.848J
The elastic potential energy stored in the spring when compressed by a distance x is given by:
EPE=12kx2
where:
- k=1960N/m (spring constant)
- x is the maximum compression of the spring.
mgh=12kx2
Substituting the values we have:
7.848J=12×1960N/m×x2
Rearranging the equation:
x2=2×7.848J1960N/m
Calculating:
x2=15.6961960≈0.008m2
Taking the square root:
x=√0.008≈0.0894m
To convert meters to centimeters, multiply by 100:
x≈0.0894m×100≈8.94cm
The maximum compression of the spring is approximately 8.94 cm.
Similar Questions
A block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant 1960Nm−1. The maximum distance through which the spring is compressed by
View SolutionA solid cylinder of mass 3kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression produced in the spring will be :
View Solution
Knowledge Check
A block of mass 2kg is propped from a heught of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5 cmB15 cmC20 cmD10 cm
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View SolutionAuto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
View SolutionAuto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
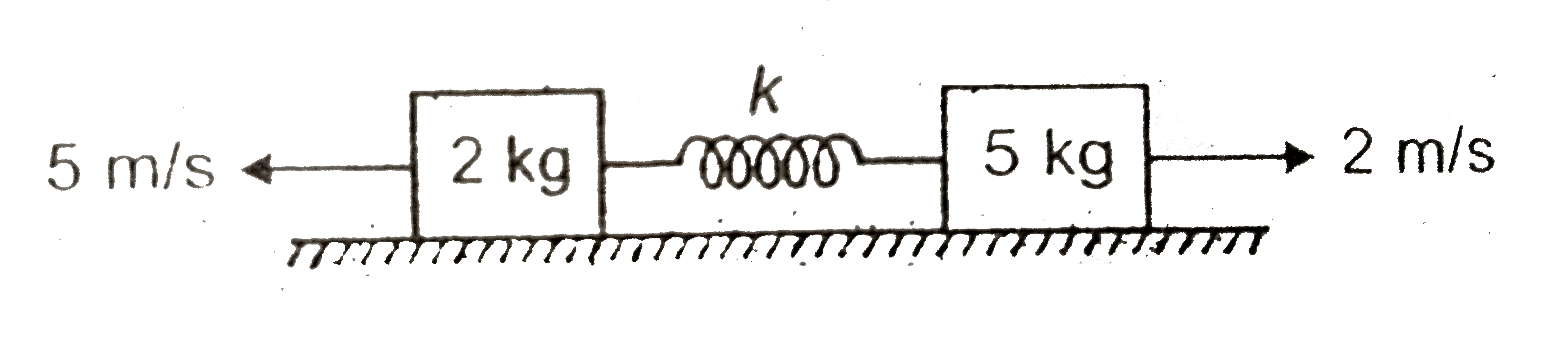
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View SolutionA body of mass 2kg collides with a horizontal weight spring of force constant 4Nm−1. The body compresses the spring by 1m from rest position. Find the speed of the block at the instant of collision ? Given that the coefficient of kinetic friction between the body and the surface is 0.1.
View Solution
