The simple pendulum bob is given a horizontal velocity √gl at the bottom. The angle with the vertical through which the ball swings before its velocity becomes zero is
120∘
60∘
45∘
30∘
The correct Answer is:B
To solve the problem, we will use the principle of conservation of mechanical energy. Let's break down the solution step by step:
Step 1: Understand the Initial Conditions
The pendulum bob is given a horizontal velocity of v=√gl at the lowest point of its swing. At this point, all the energy is kinetic energy.
Step 2: Write the Expression for Kinetic Energy
The kinetic energy (KE) at the lowest point can be expressed as:
KE=12mv2
Substituting the value of v:
KE=12m(√gl)2=12m(gl)=mgl2
Step 3: Write the Expression for Potential Energy
When the pendulum reaches its maximum height, its velocity becomes zero, and all the kinetic energy is converted into potential energy (PE). The potential energy at height h is given by:
PE=mgh
At the maximum height, the height h can be expressed in terms of the pendulum length l and the angle θ:
h=l−lcosθ=l(1−cosθ)
Thus, the potential energy can be expressed as:
PE=mg(l(1−cosθ))=mgl(1−cosθ)
Step 4: Apply Conservation of Energy
According to the conservation of mechanical energy:
KEinitial=PEfinal
Substituting the expressions we derived:
mgl2=mgl(1−cosθ)
Step 5: Simplify the Equation
We can cancel mgl from both sides (assuming m≠0 and l≠0):
12=1−cosθ
Rearranging gives:
cosθ=1−12=12
Step 6: Solve for θ
The angle θ for which cosθ=12 is:
θ=60∘
Final Answer
The angle with the vertical through which the ball swings before its velocity becomes zero is θ=60∘.
---
The pendulum bob is given a horizontal velocity of v=√gl at the lowest point of its swing. At this point, all the energy is kinetic energy.
The kinetic energy (KE) at the lowest point can be expressed as:
KE=12mv2
Substituting the value of v:
KE=12m(√gl)2=12m(gl)=mgl2
When the pendulum reaches its maximum height, its velocity becomes zero, and all the kinetic energy is converted into potential energy (PE). The potential energy at height h is given by:
PE=mgh
At the maximum height, the height h can be expressed in terms of the pendulum length l and the angle θ:
h=l−lcosθ=l(1−cosθ)
Thus, the potential energy can be expressed as:
PE=mg(l(1−cosθ))=mgl(1−cosθ)
According to the conservation of mechanical energy:
KEinitial=PEfinal
Substituting the expressions we derived:
mgl2=mgl(1−cosθ)
We can cancel mgl from both sides (assuming m≠0 and l≠0):
12=1−cosθ
Rearranging gives:
cosθ=1−12=12
The angle θ for which cosθ=12 is:
θ=60∘
The angle with the vertical through which the ball swings before its velocity becomes zero is θ=60∘.
Similar Questions
The bobo of a pendulum at rest is given a sharp hit to impart a horizontal velocity u where l is the length of the pendulum. Find the angle rotated by the string before it becomes slack.
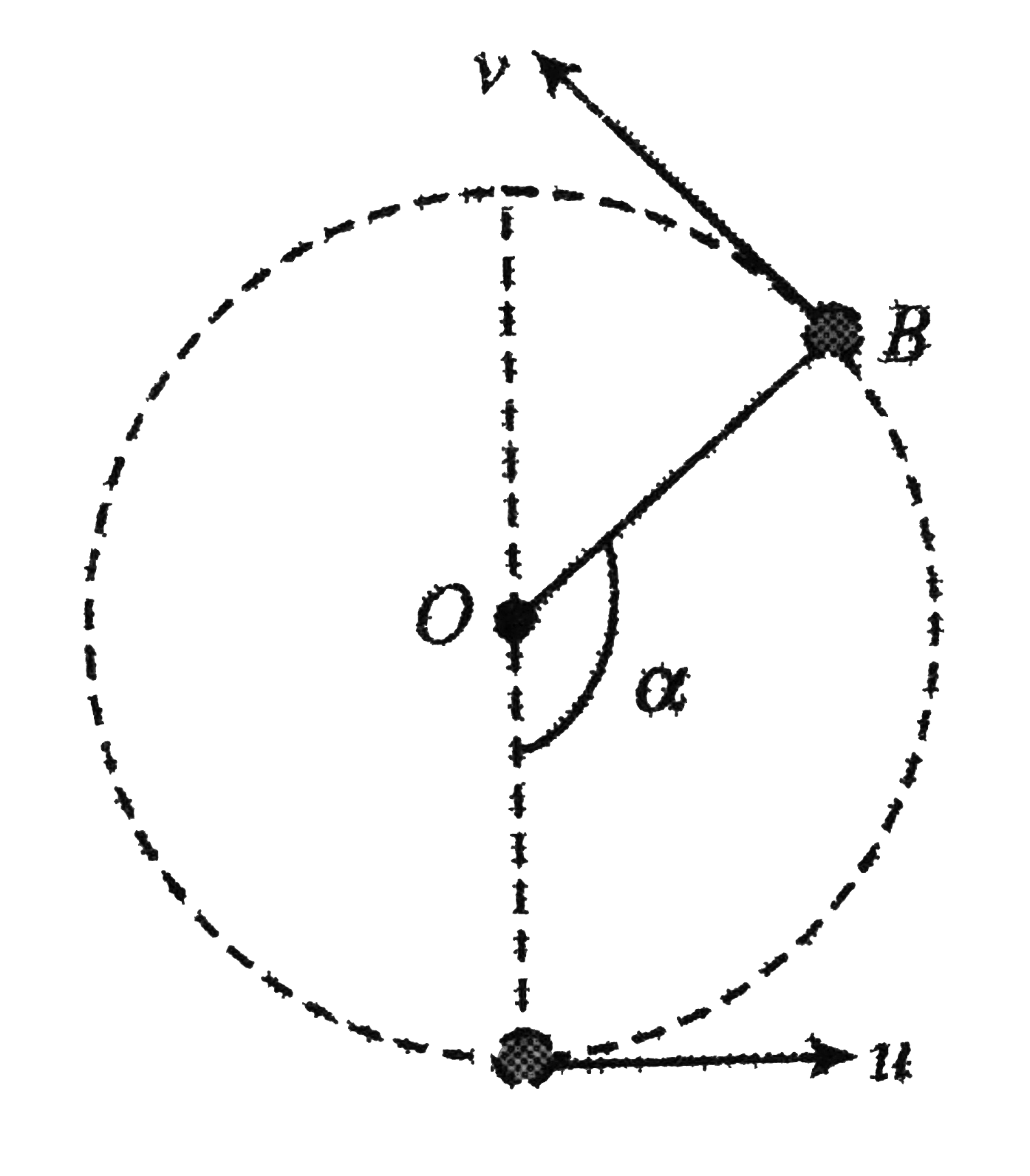
View SolutionThe bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.

View SolutionThe bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of √3gl. Find the angle rotated by the string before it becomes slack.
View SolutionA bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II

View SolutionA heavy particle hangs from a point O, by a string of length a. It is projected horizontally with a velocity u=√(2+√3)ag . The angle with the downward vertical, string makes where string becomes slack is :
View SolutionA ball of mass 'm' is suspended from a point with a massless string of length l in form of a pendulum. This ball is given a horizontal velocity √4gl at bottom most point. When string makes an angle 60∘ from lower vertical, acat=p. write the value of p2. (g=10m/s2)
View SolutionThe bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
View SolutionBob B of the pendulum AB is given an initial velocity √3Lg in horizontal direction. Final the maximum height of the bob from the starting point,
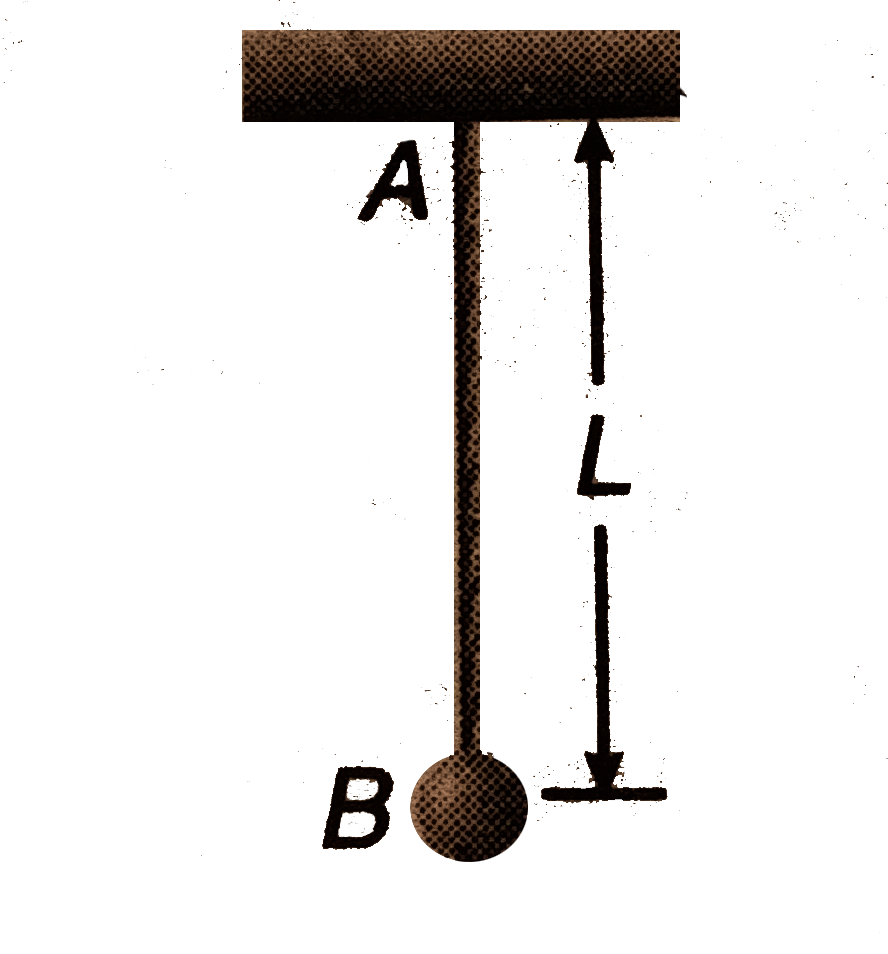
(a) if AB is a massless rod,
(b) if AB is a massless staring.
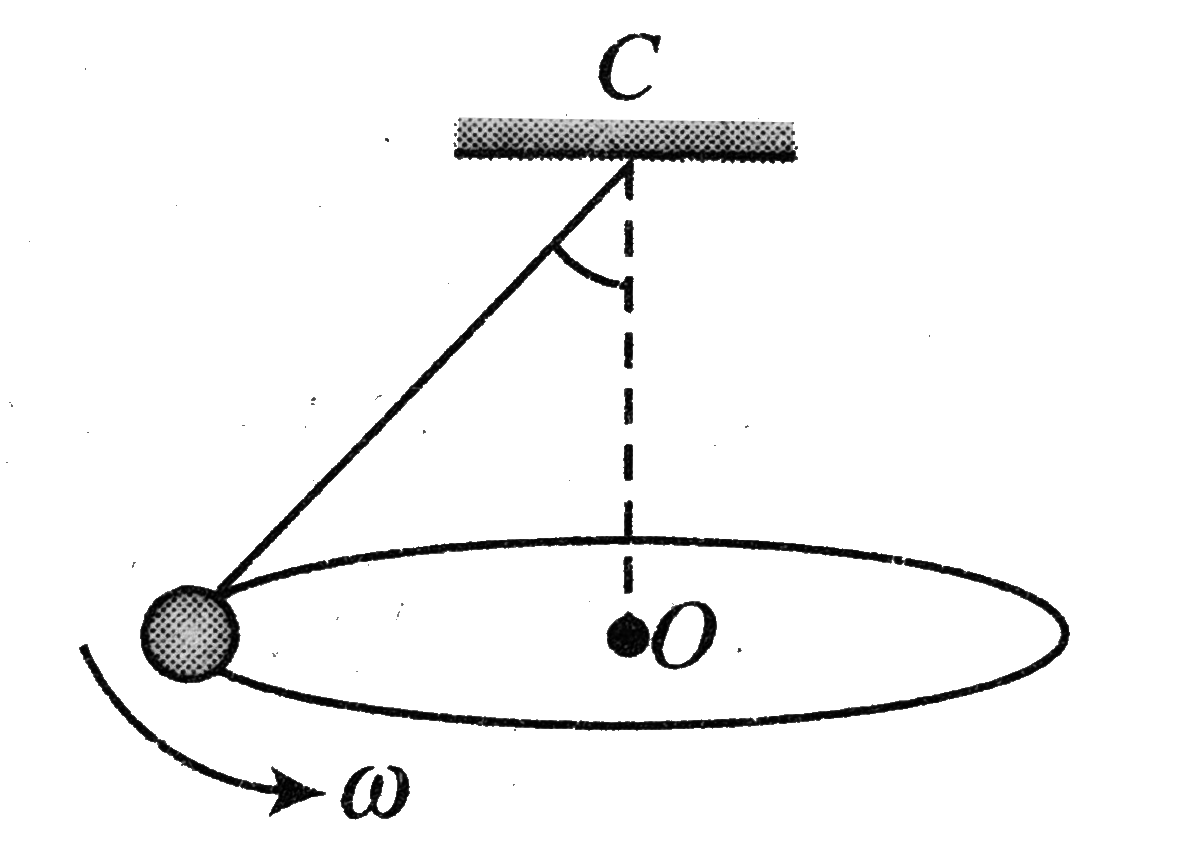
View SolutionA conical pendulum consists of a simple pendulum moving in a horizontal circle as shown in the figure. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω the constant angular velocity of the bob. If →L is the angular momentum about point C, then
View SolutionA boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View Solution