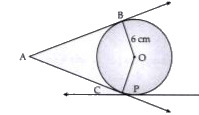
ABCD is a cyclic quadrilateral. PBQ is a tangent drawn from the point B of the circle, if ∠DBP=65∘, then measures of ∠BCD is
65∘
90∘
110∘
115∘
The correct Answer is:D
To solve the problem, we need to find the measure of angle BCD in the cyclic quadrilateral ABCD, given that angle DBP is 65 degrees.
1. Understand the Given Information:
- ABCD is a cyclic quadrilateral.
- PBQ is a tangent to the circle at point B.
- Angle DBP = 65 degrees.
2. Draw the Figure:
- Draw the cyclic quadrilateral ABCD.
- Mark the tangent PBQ at point B.
- Label the angles as given in the problem.
3. Identify Angles:
- Since PBQ is a tangent to the circle at point B, the radius OB is perpendicular to the tangent PB. Therefore, angle OBD + angle DBP = 90 degrees.
- Let angle OBD be denoted as θ. Then:
θ+65∘=90∘
- Solving for θ:
θ=90∘−65∘=25∘
4. Use Isosceles Triangle Properties:
- In triangle OBD, OB = OD (both are radii of the circle).
- Therefore, triangle OBD is isosceles, which means angles OBD and ODB are equal.
- Let angle OBD = angle ODB = θ=25∘.
5. Find Angle DOB:
- The sum of angles in triangle OBD is:
Angle OBD+Angle ODB+Angle DOB=180∘
- Substituting the known angles:
25∘+25∘+Angle DOB=180∘
- Therefore:
Angle DOB=180∘−50∘=130∘
6. Relate Angle DAB to Angle DOB:
- Since angle DAB subtends the same arc as angle DOB at the circumference, we have:
Angle DAB=12×Angle DOB=12×130∘=65∘
7. Use the Cyclic Quadrilateral Property:
- In cyclic quadrilateral ABCD, the opposite angles are supplementary:
Angle DAB+Angle BCD=180∘
- Substituting the known value:
65∘+Angle BCD=180∘
- Therefore:
Angle BCD=180∘−65∘=115∘
Final Answer:
The measure of angle BCD is 115∘.
- ABCD is a cyclic quadrilateral.
- PBQ is a tangent to the circle at point B.
- Angle DBP = 65 degrees.
- Draw the cyclic quadrilateral ABCD.
- Mark the tangent PBQ at point B.
- Label the angles as given in the problem.
- Since PBQ is a tangent to the circle at point B, the radius OB is perpendicular to the tangent PB. Therefore, angle OBD + angle DBP = 90 degrees.
- Let angle OBD be denoted as θ. Then:
θ+65∘=90∘
- Solving for θ:
θ=90∘−65∘=25∘
- In triangle OBD, OB = OD (both are radii of the circle).
- Therefore, triangle OBD is isosceles, which means angles OBD and ODB are equal.
- Let angle OBD = angle ODB = θ=25∘.
- The sum of angles in triangle OBD is:
Angle OBD+Angle ODB+Angle DOB=180∘
- Substituting the known angles:
25∘+25∘+Angle DOB=180∘
- Therefore:
Angle DOB=180∘−50∘=130∘
- Since angle DAB subtends the same arc as angle DOB at the circumference, we have:
Angle DAB=12×Angle DOB=12×130∘=65∘
- In cyclic quadrilateral ABCD, the opposite angles are supplementary:
Angle DAB+Angle BCD=180∘
- Substituting the known value:
65∘+Angle BCD=180∘
- Therefore:
Angle BCD=180∘−65∘=115∘
The measure of angle BCD is 115∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Maximum number of tangents drawn from a point on the circle is :
A1B2C3DNone of these. - Question 2 - Select One
Number of tangents drawn from a point inside the circle is :
A1B2C4D0 - Question 3 - Select One
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ=65∘, then ∠BCD is:
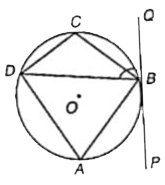 A35∘B85∘C115∘D90∘
A35∘B85∘C115∘D90∘
In Figure, ABCD is a cyclic quadrilateral; O is the centre of the circle. If ∠BOD=1600, find the measure of ∠BPD
View SolutionABCD is a cyclic quadrilateral and PQ is a tangent to the circle at C. If BD is a diameter, measure of (i) LDBC (ii) LBCP (iii) LBDC (iv) LADB
View SolutionABCD is a cyclic quadrilateral and O is the centre of the circle. If ∠COD=140∘and ∠BAC=40∘. then the value of ∠BCD is equal to
View SolutionABCD is a cyclic quadrilateral whose vertices are equidistant from the point O (centre of the circle). If ∠COD=120∘ and ∠BAC=30∘, then the measure of ∠BCD is :
View SolutionABCD is a cyclic quadrilateral whose vertices are equidistant from the point O (centre of the circle). If ∠COD=120∘ and ∠BAC=30∘, then the measure of ∠BCD is
View Solution