ABCD is a cyclic quadrilateral whose vertices are equidistant from the point O (centre of the circle). If ∠COD=120∘ and ∠BAC=30∘, then the measure of ∠BCD is
A
180∘
B
150∘
C
60∘
D
90∘
Video Solution
Text Solution
The correct Answer is:D
|
Answer
Step by step video, text & image solution for ABCD is a cyclic quadrilateral whose vertices are equidistant from the point O (centre of the circle). If angleCOD = 120^@ and angleBAC = 30^@, then the measure of angleBCD is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023
Knowledge Check
- Question 1 - Select One
In the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
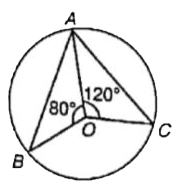 A120∘B80∘C100∘Dnone of the above
A120∘B80∘C100∘Dnone of the above - Question 1 - Select One
ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If ∠ADC=130∘, find ∠BAC.
 A40∘B50∘C60∘D30∘
A40∘B50∘C60∘D30∘ - Question 1 - Select One
ABCD is a cyclic quadrilateral. PBQ is a tangent drawn from the point B of the circle, if ∠DBP=65∘, then measures of ∠BCD is
A65∘B90∘C110∘D115∘ - Question 1 - Select One
ABCD is a cyclic quadrilateral and O is the centre of the circle. If ∠COD=140∘and ∠BAC=40∘. then the value of ∠BCD is equal to
A70∘B90∘C60∘D80∘ - Question 1 - Select One
ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
Aa) 50∘Bb) 35∘Cc) 55∘Dd) 30∘ - Question 1 - Select One
In the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
A40∘B20∘C25∘D30∘ - Question 1 - Select One
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
A80∘B50∘C40∘D30∘ - Question 1 - Select One
ABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and ∠ADC=150∘. Then. ∠BAC is equal to:
A40∘B60∘C38∘D50∘

