ABCD is a cyclic quadrilateral whose vertices are equidistant from the point O (centre of the circle). If ∠COD=120∘ and ∠BAC=30∘, then the measure of ∠BCD is :
180∘
150∘
60∘
90∘
The correct Answer is:D
To solve the problem, we need to find the measure of angle BCD in the cyclic quadrilateral ABCD, given that angle COD = 120° and angle BAC = 30°.
1. Understand the properties of cyclic quadrilaterals: In a cyclic quadrilateral, the opposite angles are supplementary. This means that the sum of the angles at opposite vertices equals 180°.
2. Identify the angles: We are given:
- Angle COD = 120°
- Angle BAC = 30°
3. Use the inscribed angle theorem: The angle subtended by an arc at the center of the circle (angle COD) is twice the angle subtended at any point on the circumference (angle BAC). Therefore, angle BCD will be equal to angle COD.
4. Calculate angle BCD: Since angle COD = 120°, angle BCD will also be equal to 120°.
5. Find angle ACD: Since angle BAC is given as 30°, we can find angle ACD using the property of cyclic quadrilaterals:
- Angle ACD = 180° - angle BAC = 180° - 30° = 150°.
6. Use the triangle properties: In triangle ODC, we know:
- Angle ODC + Angle OCD + Angle COD = 180°
- Let angle ODC = x and angle OCD = x (since they are equal).
- Therefore, we have: x + x + 120° = 180°.
- This simplifies to 2x = 60° → x = 30°.
7. Determine angle BCD: Now we know:
- Angle ACD = 30° (from step 6).
- Angle BCA = 60° (from the cyclic property).
- Thus, angle BCD = angle ACD + angle BCA = 30° + 60° = 90°.
Final Answer:
The measure of angle BCD is 90°.
- Angle COD = 120°
- Angle BAC = 30°
- Angle ACD = 180° - angle BAC = 180° - 30° = 150°.
- Angle ODC + Angle OCD + Angle COD = 180°
- Let angle ODC = x and angle OCD = x (since they are equal).
- Therefore, we have: x + x + 120° = 180°.
- This simplifies to 2x = 60° → x = 30°.
- Angle ACD = 30° (from step 6).
- Angle BCA = 60° (from the cyclic property).
- Thus, angle BCD = angle ACD + angle BCA = 30° + 60° = 90°.
The measure of angle BCD is 90°.
Topper's Solved these Questions
- QUADRILATERALBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:QUADRILATERALExercise:EXERCISE
Explore 48 Videos
- PROFIT & LOSSBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:PROFIT & LOSSExercise:Questions
Explore 200 Videos
- RATIO & PROPORTIONBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:RATIO & PROPORTIONExercise:QUESTIONS
Explore 113 Videos
Similar Questions
Knowledge Check
ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If ∠ADC=130∘, find ∠BAC.
 A40∘B50∘C60∘D30∘
A40∘B50∘C60∘D30∘ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
A80∘B50∘C40∘D30∘In the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
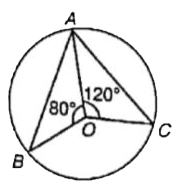 A120∘B80∘C100∘Dnone of the above
A120∘B80∘C100∘Dnone of the above
In the adjoining figure, ABCD is a cyclic quadrilateral. If ∠DBC=60∘ and ∠BAC=40∘ , then find the value of ∠BCD .
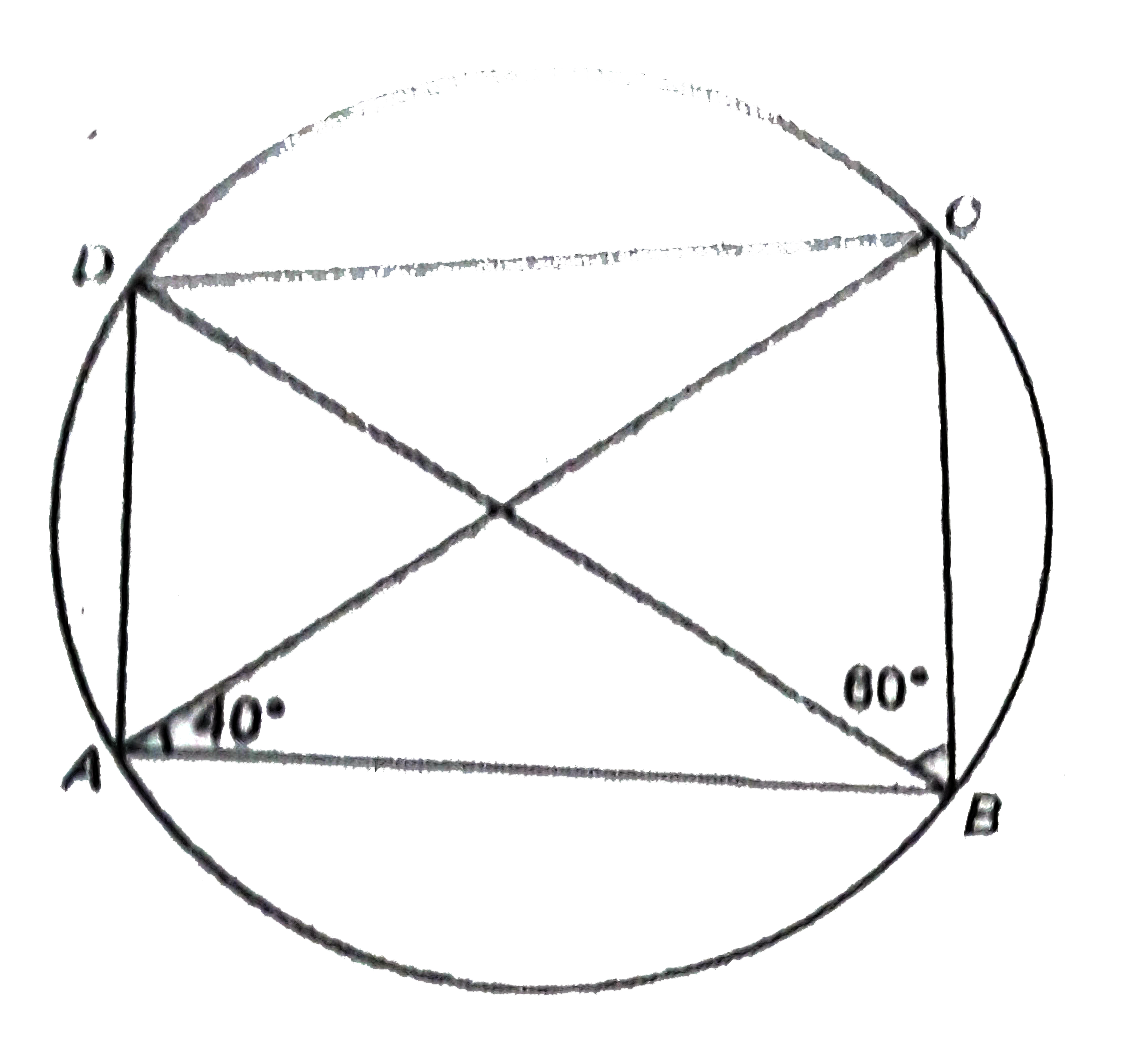
View SolutionABCD is a cyclic quadrilateral. PBQ is a tangent drawn from the point B of the circle, if ∠DBP=65∘, then measures of ∠BCD is
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
View SolutionIn the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
View SolutionABCD is a cyclic quadrilateral and O is the centre of the circle. If ∠COD=140∘and ∠BAC=40∘. then the value of ∠BCD is equal to
View Solution
