If P, R, T are the area of a Parallelogram, a rhombus and a triangle standing on the same base and between the same parallels, which of the following is true ?
R<P<T
P>R>T
R=P=T
R=P=2T
The correct Answer is:D
To solve the problem, we need to analyze the areas of a parallelogram, a rhombus, and a triangle that share the same base and are between the same parallels. Let's denote the areas as follows:
- Let P be the area of the parallelogram.
- Let R be the area of the rhombus.
- Let T be the area of the triangle.
1. Understanding the Relationship Between Areas:
- The area of a triangle that shares the same base and height as a parallelogram is half the area of the parallelogram. Therefore, we can express this relationship mathematically:
T=12P
2. Area of the Rhombus:
- A rhombus can be considered a special type of parallelogram. Since the rhombus also shares the same base and height, its area is equal to that of the parallelogram:
R=P
3. Substituting the Area of the Rhombus:
- From the first equation, we have T=12P. From the second equation, we have R=P. We can substitute R into the first equation:
T=12R
4. Expressing All Areas in Terms of T:
- We can express P and R in terms of T:
- From T=12P, we can rearrange to find P:
P=2T
- Since R=P, we also have:
R=2T
5. Final Relationships:
- Now we can summarize the relationships:
R=P=2T
Conclusion:
From our analysis, we conclude that:
R=P=2T
- Let R be the area of the rhombus.
- Let T be the area of the triangle.
- The area of a triangle that shares the same base and height as a parallelogram is half the area of the parallelogram. Therefore, we can express this relationship mathematically:
T=12P
- A rhombus can be considered a special type of parallelogram. Since the rhombus also shares the same base and height, its area is equal to that of the parallelogram:
R=P
- From the first equation, we have T=12P. From the second equation, we have R=P. We can substitute R into the first equation:
T=12R
- We can express P and R in terms of T:
- From T=12P, we can rearrange to find P:
P=2T
- Since R=P, we also have:
R=2T
- Now we can summarize the relationships:
R=P=2T
From our analysis, we conclude that:
R=P=2T
Topper's Solved these Questions
- QUADRILATERALBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:QUADRILATERALExercise:EXERCISE
Explore 48 Videos
- PROFIT & LOSSBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:PROFIT & LOSSExercise:Questions
Explore 200 Videos
- RATIO & PROPORTIONBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:RATIO & PROPORTIONExercise:QUESTIONS
Explore 113 Videos
Similar Questions
Knowledge Check
Which of the following figures lie on the same base and between the same parallels ?
A B
B C
C Dall of these
Dall of theseWhich of the following figures lie on the same base and between the same parallels?
A B
B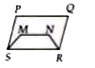 C
C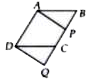 DBoth (a) and (c)
DBoth (a) and (c)Two parallelograms stand on equal bases and between the same parallels. The ratio of their areas is :
A1:1B√2:1C1:3D1:2
A ||gm and a rectangle on the same base and between the same parallels are equal in area
View SolutionTwo Triangle having the same base and equal areas lie between the same parallels.
View SolutionIf two triangles are on the same base and between the same parallels. Then find the ratio of area of the two triangles.
View SolutionProve that parallelograms on the same base and between the same parallels have the same area.
View SolutionParallelograms on the same base and between the same parallel are equal in area.
View Solution
