A monatomic ideal gas is contained in a rigid container of volume V with walls of total inner surface area A, thickness x and thermal conductivity K. The gas is at an initial temperature and pressure . Find the pressure of the gas as a function of time if the temperature of the surrounding air is . All temperature are in absolute scale. Solution in Tamil
As the volume of the gas is constant, a heat deltaT=DeltaQ//C_(v) . If the temperature ot the gas at time t is T, the heat current into the gas is
. or, . or, . or, . or, . As the volume remains constant, . or, . .
Topper's Solved these Questions
- HEAT TRANSFERBook:HC VERMAChapter:HEAT TRANSFERExercise:QUESTIONS FOR SHORT ANSWER
Explore 11 Videos
- HEAT TRANSFERBook:HC VERMAChapter:HEAT TRANSFERExercise:OBJECTIVE I
Explore 10 Videos
- HEAT TRANSFERBook:HC VERMAChapter:HEAT TRANSFERExercise:EXERCIESE
Explore 55 Videos
- HEAT AND TEMPERATUREBook:HC VERMAChapter:HEAT AND TEMPERATUREExercise:Exercise
Explore 34 Videos
- INTRODUCTION TO PHYSICSBook:HC VERMAChapter:INTRODUCTION TO PHYSICSExercise:Exercises
Explore 19 Videos
Similar Questions
The heat current is written as ΔQΔt . Why don't we write dQdt ?
View SolutionThe thermal conductivity of a rod depends on
View SolutionA uniform slab of dimension 10cm×10cm×1cm is kept between two heat reservoir at temperatures 10∘C and 90∘C. The larger surface areas touch the reservoirs. The thermal conductivity of the material is 0.80Wm−1C−1 . Find the amount of heat flowing through the slab per minute.
View SolutionThe steam point and the ice point of a mercury thermometer are marked as 80∘C and 20∘C. What will be the temperature in centigrade mercury scale when this thermometer reads 32∘C?
View SolutionFind the dimensions of
a. linear momentum
b. frequency and
c. pressure
View SolutionAn amount n (in moles) of a monatomic gas at initial temperature T_(0) is enclosed in a cylinderical vessel fitted with a ligth piston. The surrounding air has a temperature T_(s)(gtT_(0)) . And the atmospheric pressure is P_(a) . Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all change to be slow, find the distance moved by the piston in time t.
View SolutionA quantity of gas occupies an initial volume V_(0) at pressure p_(0) and temperature T_(0) . It expands to a volume V (a) constant temperature and (b) constant pressure. In which case does the gas do more work ?
View SolutionA temperature T is measured by a constant volume gas thermometer (i) T is independent of the gas used at all pressure (ii) T is independent of the gas used only at low pressure (iii) The ideal gas scale agrees with the absolute scale of temperature (iv) The ideal gas scale does not agrees with the absolute scale of temperature
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p_(0) and absolute temperature T_(0) . One container is now maintained at the same temperature while the other is heated to 2T_(0) . The common pressure of the gas
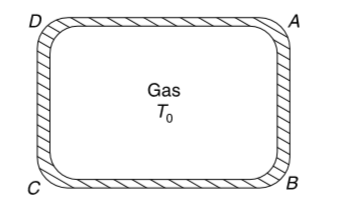
View SolutionAn ideal gas at temperature T0 is contained in a container. By some mechanism, the temperature of the wall AB is suddenly increased to T(>T0). Will the pressure exerted by the gas on wall AB change suddenly? Will it be higher or lower than pressure on wall CD?
View SolutionA container of volume V_(1) has an ideal gas of molar mass M_(1) at pressure P_(1) and temperature T_(1) . Another container of volume V_(2) has another ideal gas of molar mass M_(2) at pres- sure P_(2) and temperature T_(2) . Two gases are mixed in a vessel and acquire an equilibrium temperature and pressure of T_(0) and P_(0) respectively. Find the density of the mixture.
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T_(0) and pressure P_(0) occupies a volume V_(0) in the cylinder. The atmospheric pressure is P_(0) and the atmospheric temperature is T_(1) (gt T_(0)) . Find (a) the temperature of the gas as a function of time (b) the height raised by the piston as a function of time. Neglect friction and heat capacities of the container and the piston.
View SolutionAn ideal gas in thermally insulated vessel at internal (pressure)=P_(1), (volume)=V_(1) and absolute temperature = T_(1) expands irreversiby against zero external, pressure , as shown in the diagram, The final internal pressure, volume and absolute temperature of the gas are p_(2), V_(2) and T_(2) , respectively . For this expansion
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
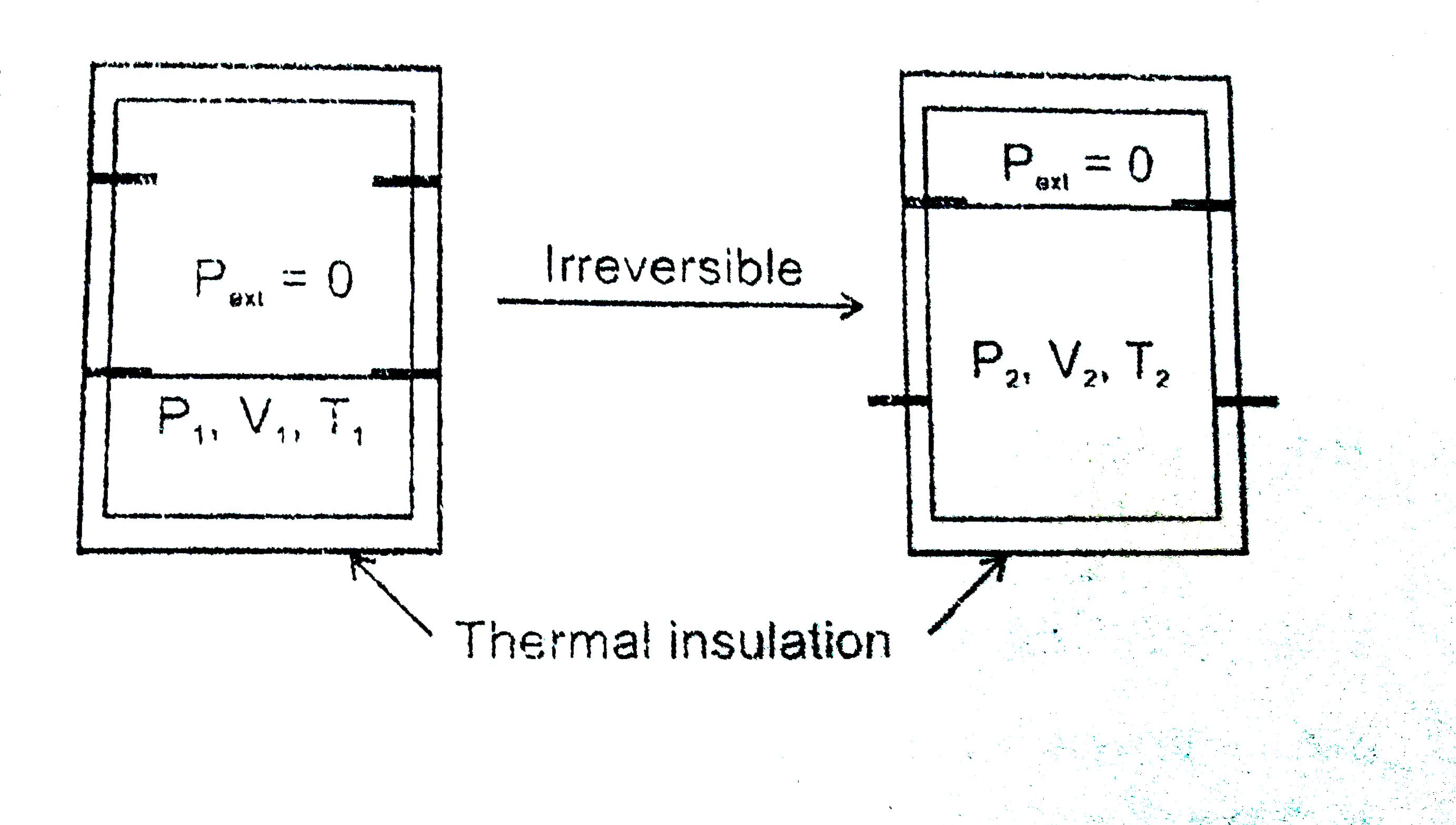
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P4, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
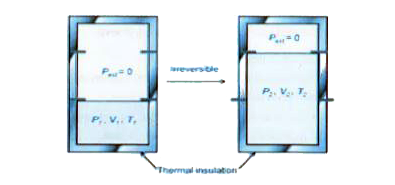
View SolutionAn amount n (in moles) of a monatomic gas at initial temperature T_(0) is enclosed in a cylindrical vessel fitted with a light piston. The surrounding air has a temperature T_(s)(gtT_(0)) . And the atmospheric pressure is P_(a) . Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all change to be slow, find the distance moved by the piston in time t.
View Solution