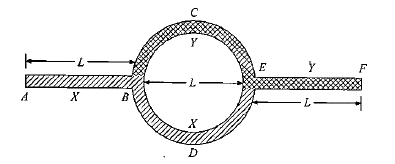
Three rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at $60^{\circ} C$ and the junction E at $10^{\circ} C$ , calculate the temperature of the junction B. The thermal conductivity of x is $800 W m^{- 1} C^{- 1}$ and that of y is $400 W m^{- 1} C^{- 1}$ .
Solution in Tamil

Video Solution

Text Solution

Verified by Experts

It is clear from the symmerty of the figure that the points C and D are equivalent in all respect and hence, they are at the same temperature, say (theta). No heat will flow through the rod CD. We can, therefore, neglect this rod in further analysis.
Let l and A be the length and the area of cross section of each rod. The thermal resistances of AB, BC and BD are equal. Each has a value
$R_{1} = \frac{1}{K_{x}} \frac{l}{A}$ . Similarly, thermal resistances of CE and DE are equal, each having a value
$R_{2} = \frac{1}{K_{y}} \frac{l}{A}$ . As the rod CD has no effect, we can say that the rods BC and CE are joined in sseries. Their equivalent thermal resistance is
$R_{3} = R_{B C} + (R_{C E} = R_{1} + R_{2}$ . Also, the rods BD and DE together have an equivalent thermal resistance $R_{4} = R_{B D} + (R_{D E} = R_{1} + R_{2}$ . The resistance $R_{3}$ and $R_{4}$ are joined in paralley and hence their equivalent thermal resistance is given by
$\frac{1}{R_{5}} = \frac{1}{R_{3}} + \frac{1}{R_{4}} = \frac{1}{R_{3}}$ . or, $= R_{5} = \frac{R_{3}}{2} = \frac{R_{1} + R_{2}}{2}$ . This resistance $R_{5}$ is connected in series with AB. Thus, the total arrangement is equivalent to a thermal resistance
$R = R_{A B} + R_{5} = R_{1} + \frac{R_{1} + R_{2}}{2} = \frac{3 R_{1} + R_{2}}{2}$ . Figure shows the successive steps in this reduction.
. The heat current through A is
$i = \frac{θ_{A} - θ_{E}}{R} = \frac{2 (θ_{A} - θ_{E})}{3 R_{1} + R_{2}}$ . This current passes through the rod AB. We have
$i = \frac{θ_{A} - θ_{B}}{R_{A B}}$ .or, $θ_{A} - θ_{B} = (R_{A B}) i$ . $= R_{1} \frac{2 (θ_{A} - θ_{E})}{3 R_{1} + R_{2}}$ . Putting from (i) and (ii), $θ_{A} - θ_{B} = \frac{2 K_{y} (θ_{A} - θ_{E})}{K_{x} + R_{2}}$ . $= \frac{2 \times 400}{800 + 3 \times 400} \times 50^{\circ} C = 20^{\circ} C$ . or, $θ_{B} = θ_{A} - 20^{\circ} C = 40^{\circ} C$ .

Updated on:21/07/2023

|

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

HC VERMA-HEAT TRANSFER-worked out examples

Home
Ask Doubt
Profile