From a uniform disc of radius R, a circular disc of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of original disc. Locate the centre of gravity of the resultant flat body. Solution in Tamil
Let the centre of the bigge disc be the origin.
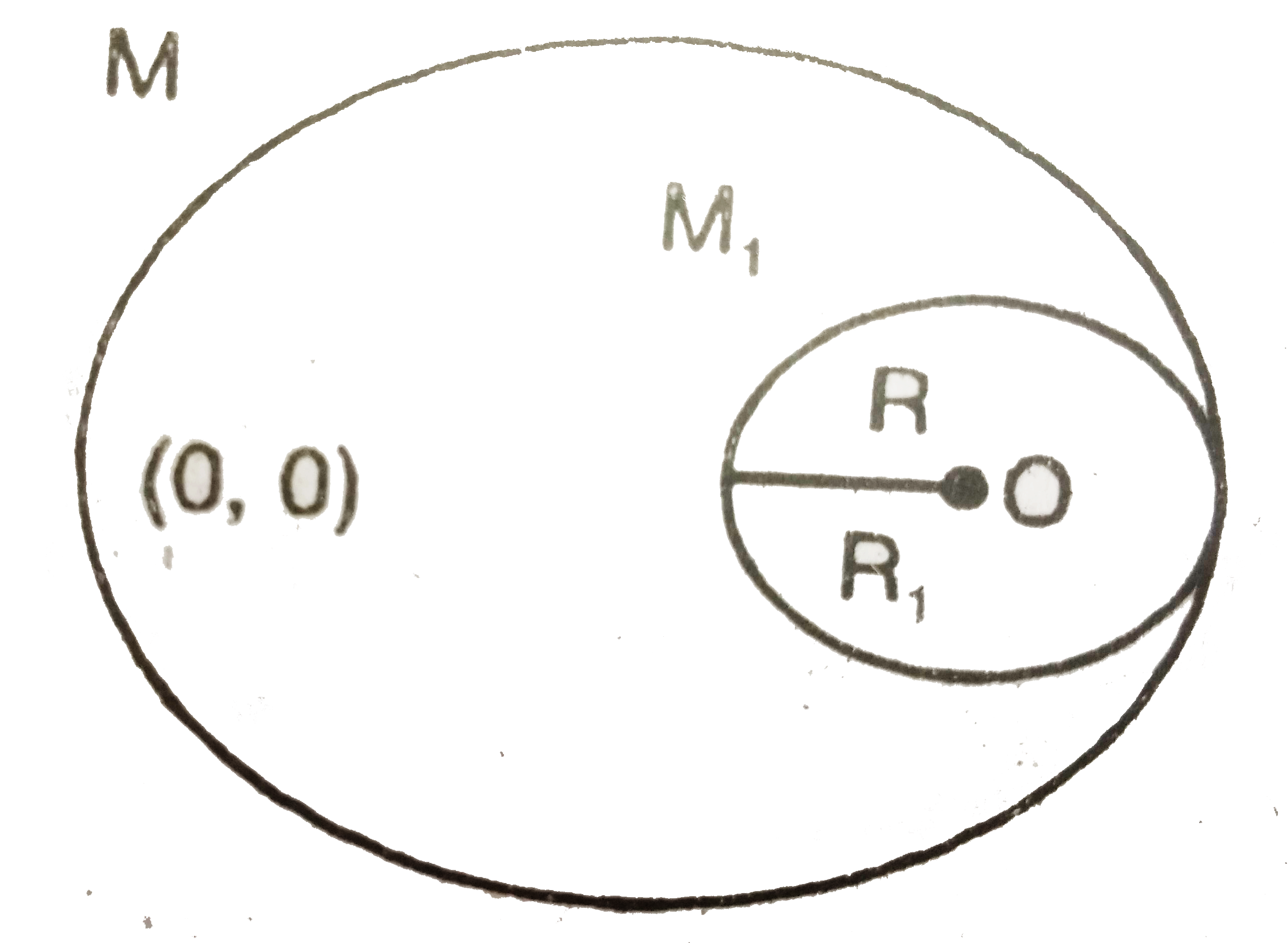
rho=Density of the two discs:.((m_1x_1+m_2x_2)/(m_1+m_2),(m_1y_1+m_2y_2)/(m_1+m_2))x_1=R,y_1=0x_2=0, y_2=0((piR^2TrhoR+0)/(muR^2TrhoR+mu(2R)^2Trho),0/(m_1+m_2))((piR^2TrhoR)/(5muR^2Trho))=(R/4,0)R/5 from the centre of bigger disc towards.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMAChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- CALORIMETRYBook:HC VERMAChapter:CALORIMETRYExercise:Exercises
Explore 18 Videos
- CIRCULAR MOTIONBook:HC VERMAChapter:CIRCULAR MOTIONExercise:Exercises
Explore 30 Videos
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
View SolutionFigure shows a uniform disc of radius R , from which a hole of radius R/2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionA circular section of radius r si cut out of a uniform disc of radius R, the centre of the hole being R/2 from the centre of the original disc. Locate the centre of gravity of the remainder.
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA circular disc of radius (R)/(4) is cut from a uniform circular disc of radius R. The centre of cut portion is at a distance of (R)/(2) from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.
View SolutionA uniform disc of radius R has a hole cut out which has a radius r. The centre of hole is at a distance (R )/(2) from the centre of disc. The position of centre of mass is :
View SolutionFrom a uniform disc of radius R, a circular disc of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of original disc. Locate the centre of gravity of the resultant flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View Solution

