Triangle PQR is inscribed in a circle, center at O such that ∠Q=70∘and∠R=55∘. PT is perpendicular to QR and the line OP touches the side QR at the point S. Find ∠TPS
15/2∘
15∘
20∘
30∘
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have triangle PQR inscribed in a circle with center O. We know:
- Angle Q = 70°
- Angle R = 55°
- PT is perpendicular to QR
- OP touches QR at point S
Step 2: Find angle P
To find angle P, we use the fact that the sum of angles in a triangle is 180°.
Angle P=180°−Angle Q−Angle R
Substituting the values:
Angle P=180°−70°−55°=55°
Step 3: Analyze triangle PQT
In triangle PQT, we know:
- Angle PTQ = 90° (since PT is perpendicular to QR)
- Angle PQT = Angle Q = 70°
Now we can find angle QPT:
Angle QPT=180°−Angle PTQ−Angle PQT
Substituting the values:
Angle QPT=180°−90°−70°=20°
Step 4: Find angle POR
Angle POR is the central angle corresponding to angle PQR. By the property of circles, the central angle is twice the inscribed angle:
Angle POR=2×Angle PQR=2×70°=140°
Step 5: Use the isosceles triangle property
In triangle POR, OP = OR (both are radii of the circle). Therefore, angles OPR and ORP are equal. Let’s denote them as x:
Angle OPR=Angle ORP=x
Using the triangle sum property:
Angle POR+Angle OPR+Angle ORP=180°
Substituting the known values:
140°+x+x=180°
2x=40°⟹x=20°
Thus, Angle OPR = Angle ORP = 20°.
Step 6: Find angle TPS
Now we will find angle TPS using the angles in triangle PTS:
Angle P=Angle QPT+Angle TPS+Angle SPR
We know:
- Angle P = 55°
- Angle QPT = 20°
- Angle SPR = Angle OPR = 20°
Substituting the values:
55°=20°+Angle TPS+20°
55°=40°+Angle TPS
Angle TPS=55°−40°=15°
Final Answer
Thus, the angle TPS is:
Angle TPS=15°
We have triangle PQR inscribed in a circle with center O. We know:
- Angle Q = 70°
- Angle R = 55°
- PT is perpendicular to QR
- OP touches QR at point S
To find angle P, we use the fact that the sum of angles in a triangle is 180°.
Angle P=180°−Angle Q−Angle R
Substituting the values:
Angle P=180°−70°−55°=55°
In triangle PQT, we know:
- Angle PTQ = 90° (since PT is perpendicular to QR)
- Angle PQT = Angle Q = 70°
Angle QPT=180°−Angle PTQ−Angle PQT
Substituting the values:
Angle QPT=180°−90°−70°=20°
Angle POR is the central angle corresponding to angle PQR. By the property of circles, the central angle is twice the inscribed angle:
Angle POR=2×Angle PQR=2×70°=140°
In triangle POR, OP = OR (both are radii of the circle). Therefore, angles OPR and ORP are equal. Let’s denote them as x:
Angle OPR=Angle ORP=x
Using the triangle sum property:
Angle POR+Angle OPR+Angle ORP=180°
Substituting the known values:
140°+x+x=180°
2x=40°⟹x=20°
Thus, Angle OPR = Angle ORP = 20°.
Now we will find angle TPS using the angles in triangle PTS:
Angle P=Angle QPT+Angle TPS+Angle SPR
We know:
- Angle P = 55°
- Angle QPT = 20°
- Angle SPR = Angle OPR = 20°
55°=20°+Angle TPS+20°
55°=40°+Angle TPS
Angle TPS=55°−40°=15°
Thus, the angle TPS is:
Angle TPS=15°
Similar Questions
Knowledge Check
Triangle PQR circumscribes a circle with centre O and radius r cm such that ∠PQR=90∘. If PQ=3cm,QR=4cm, then the value of r is :
A2B1.5C2.5D1In a triangle PQR, S and T lie on PQ and PR, respectively, such that ∠QSR=∠PRQ and ∠QTR=∠PQR. And, PQ = 12, QR = 9, PR = 15. Find the value of PS×PT
AA)50.4BB)52.64CC)49.75DD)none of thesePQR is a triangle in which PR=QR. Side PR is extended to S, such that QR=RS. If ∠QPR=40∘, then what is the value (in degrees) of ∠QSR?
 A45B50C55D41
A45B50C55D41
AABC is inscribed in a circle. Point P lies on a circumscribed circle of a triangle be such that through point P. PN, PM and PL are perpendicular on sides of triangle (possibly by increasing sides). Prove that points N, M and L are collinear.
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionIn △PQR, the side QR is extended to S such that RS = PR. If ∠QPS=110∘ and ∠PRQ=70∘, then the value of ∠PQR is:
PQR में, भुजा QR को S तक बढ़ाया जाता है ऐसा कि RS = PR. यदि ∠QPS=110∘ और ∠PRQ=70∘, तो ∠PQR का मान है:
View SolutionIn Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR=189cm2, then find the lengths of sides PQ and PR.
View SolutionIn the figure given figure, PQRS is a square inscribed in a circle of radius 4 cm. PQ is produced till point Y. From Y a tangent in drawn to the circle at point R (QR=QY). What is the length (in cm) of SY?
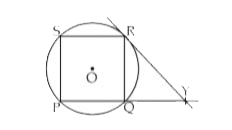
View Solution
