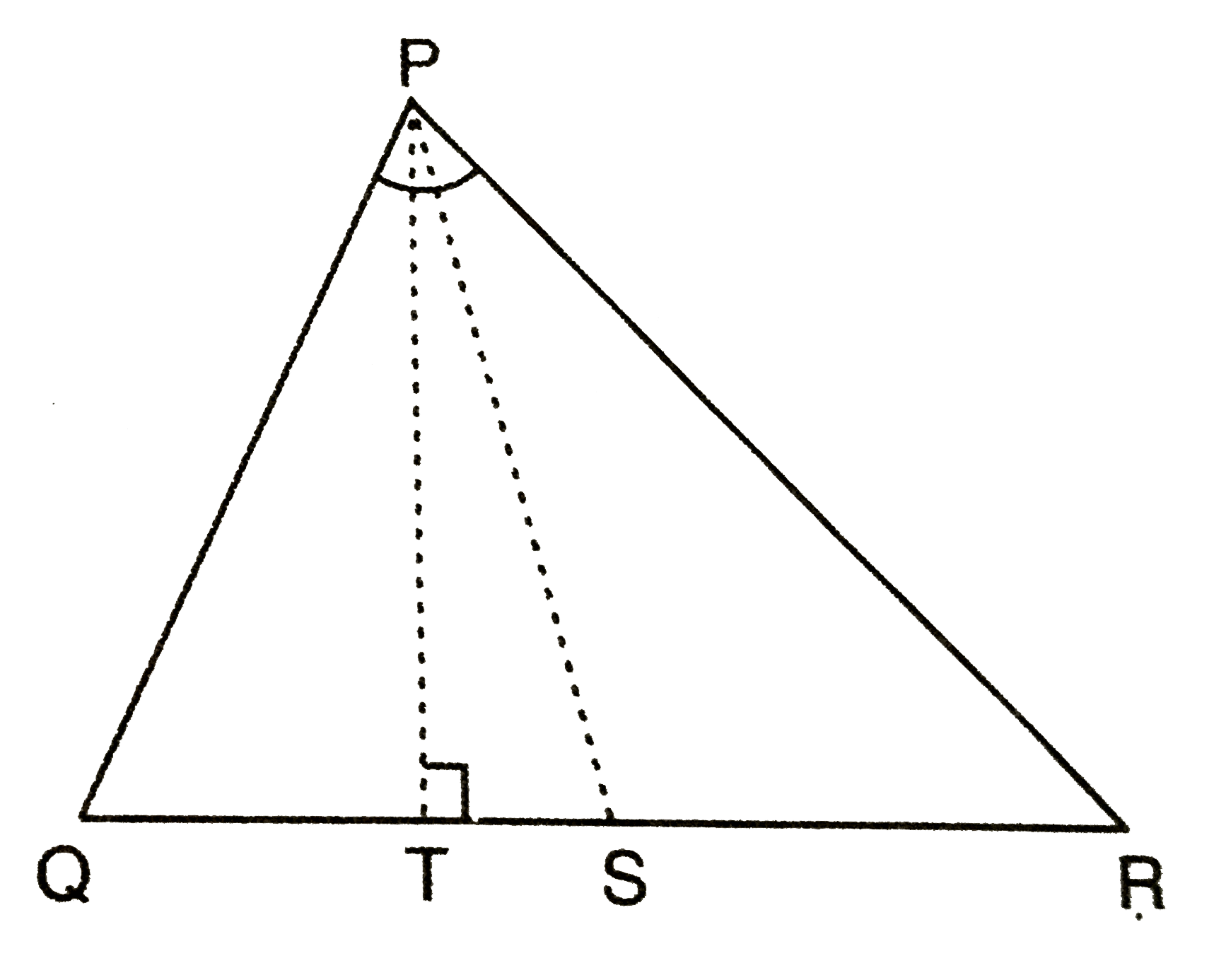
चित्र 9.7 में, ∠QPR का अर्धक PS है तथा PT भुजा QR पर लम्ब है, तो सिद्ध कीजिए किः ∠TPS=12(∠Q−∠R)
चूँकि ∠QPR का अर्धक PS है। अतः
∠QPS=∠SPR … (i)
त्रिभुज PQT में कोण योग गुणधर्म लगाने पर
∠PQT+∠PTQ+∠QPT=180∘
⇒∠PQT+90∘+∠QPT=180∘
⇒∠PQT+∠QPT=90∘
⇒∠PQT=90∘−∠QPT
⇒∠Q=90∘−∠QPT
ΔPTR मे कोण योग गुणधर्म लगाने पर
∠PRT+∠TPR+∠PTR=180∘
⇒∠PRT+∠TPR+90∘=180∘
⇒∠PRT+∠TPR=90∘
⇒∠PRT=90∘−∠TPR
⇒∠R=90∘−∠TPR ... (iii)
(ii) में (iii) से घटाने पर
∠Q−∠R=(90∘−∠QPT)−(90∘−∠TPR)
⇒∠Q−∠R=∠TPR−∠QPT
⇒∠Q−∠R=(∠TPS+∠SPR)−(∠QPS−∠TPS)
⇒∠Q−∠R=2∠TPS [∵∠QPS=∠SPR,(i) से]
⇒∠TPS=12(∠Q−∠R)
Topper's Solved these Questions
- त्रिभुज तथा उसके कोण Book:RD SHARMAChapter:त्रिभुज तथा उसके कोण Exercise:प्रश्नावली 9.1
Explore 17 Videos
- त्रिभुज तथा उसके कोण Book:RD SHARMAChapter:त्रिभुज तथा उसके कोण Exercise:प्रश्नावली 9.2
Explore 28 Videos
- चतुभुर्ज Book:RD SHARMAChapter:चतुभुर्ज Exercise:बहु विकल्पीय प्रश्न
Explore 32 Videos
- दो चरो वाले रैखिक समीकरण Book:RD SHARMAChapter:दो चरो वाले रैखिक समीकरण Exercise:बहु विकल्पीय प्रश्न
Explore 10 Videos
Similar Questions
एक ΔABC में, यदि ∠A=55∘,∠B=40∘, तो ∠C ज्ञात कीजिए।
View Solutionयदि किसी त्रिभुज के आधार को दोनों दिशाओं में आगे बढ़ाने पर प्राप्त बहिष्कोणो के मान 104∘ तथा 136∘ है, तो त्रिभुज के सभी कोण ज्ञात कीजिए।
View Solutionकिसी चतुभुर्ज में सम्मुख भुजाओं के लिए
View Solutionयदि (4,19) समीकरण y=ax+3 का एक हल है तो , a का मान है:
View SolutionIn the given figure, PS=PR,∠TPS=∠QPR. Prove that PT=PQ.
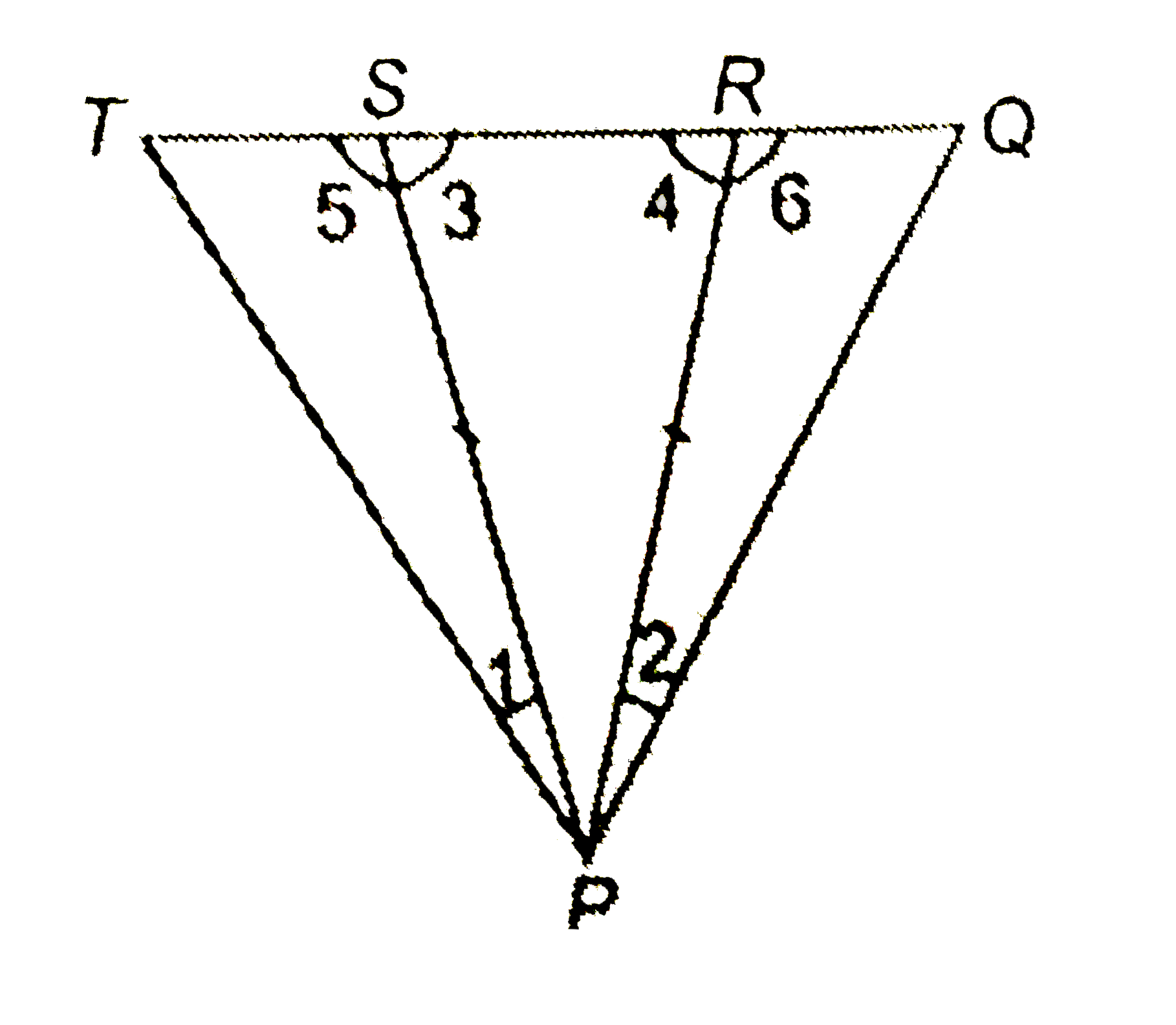
View Solutionनीचे के चित्र में PS=PR,∠TPS=∠QPR. साबित करें कि PT = PQ.
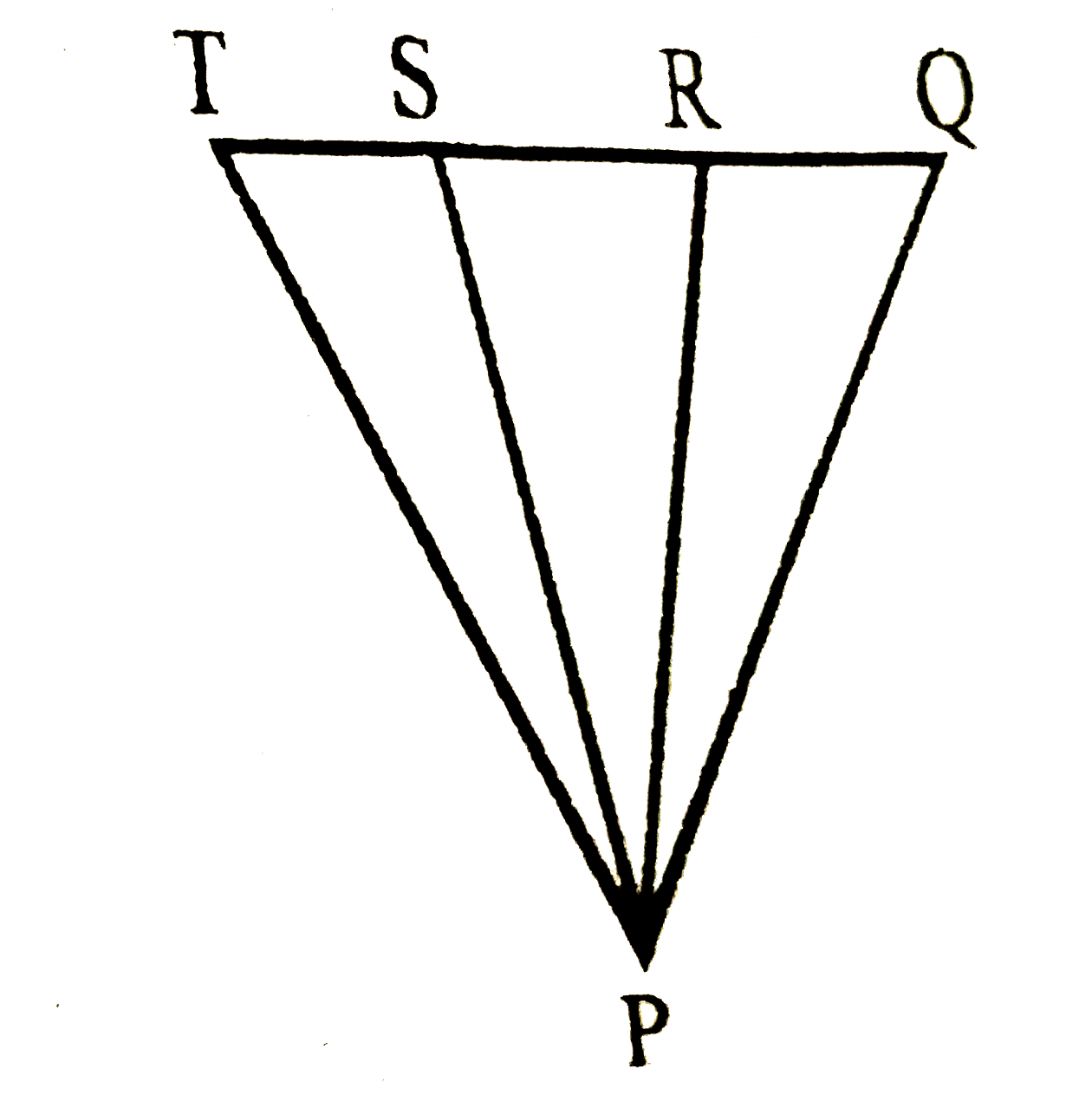
View Solutionयदि p मूलबिंदु से रेखा xa+yb=1 पर लम्ब कि लम्बाई है तथा a2,p2,b2 समान्तर श्रेढी में है , तब सिद्ध कीजिए कि a4+b4=0
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionएक अनन्त गुणोत्तर श्रेढी का योग x है तथा श्रेढी के सभी पदों का वर्ग करने पर श्रेढी का योग y है । सिद्ध कीजिए कि श्रेढी का सार्व अनुपात x2−yx2+y है ।
View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionसिद्ध कीजिए f(x)=x2 अंतराल (0,∞) में वर्धमान तथा अंतराल (−∞,0) में हस्यमान है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solution

