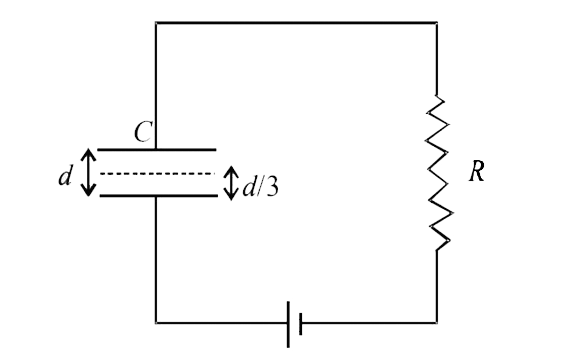
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3 initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-
6ε0R5d+3/t
(15d+9vt)ε0R2d3−3dvt−gv2t2
6ε0R5d−3vt
(15d−9vt)ε0R2d3+3dvt−9v2t2
The correct Answer is:A
We have the time constant, τ=RC.…(i)
Now, C.=C1C2C1+C2=(Aε0d−x)(KAε0x)Aε0d−x+KAε0x
∴C.=KAε0x+K(d−x)
Putting the value of C. in Eq (i), we get
τ=RKAε0d3−vt+k(d−d3+vt)[∵x=d3−vt]
Given, A= 1 and K=2
∴τ=3×2ε0×Rd−3vt+6d−2d+6vt=6Rε05d+3vt
Topper's Solved these Questions
Similar Questions
A parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as K=K0+αx, where K and α are constants and x is the distance from the left end. Calculate the capacitance.

View Solution
Knowledge Check
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3 initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-
 A6ε0R5d+3/tB(15d+9vt)ε0R2d3−3dvt−gv2t2C6ε0R5d−3vtD(15d−9vt)ε0R2d3+3dvt−9v2t2
A6ε0R5d+3/tB(15d+9vt)ε0R2d3−3dvt−gv2t2C6ε0R5d−3vtD(15d−9vt)ε0R2d3+3dvt−9v2t2A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0d
A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0dA parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?
 A3Kε0A4dB4Kε0A3dC(K+1)ε0A2dDK(K+3)ε0A2(K+1)d
A3Kε0A4dB4Kε0A3dC(K+1)ε0A2dDK(K+3)ε0A2(K+1)d
Two conducting plates each having area A are kept at a separation d parallel to each other. The two plates are con- nected to a battery of emf V. The space between the plates is filled with a liquid of dielectric constant K. The height (x) of the liquid between the plates increases at a uniform rate from zero to d in a time interval t0.
(a) Write the capacitance of the system as a function of x as the liquid beings to fill the space between the plates.
(b) write the current through the cell at time t
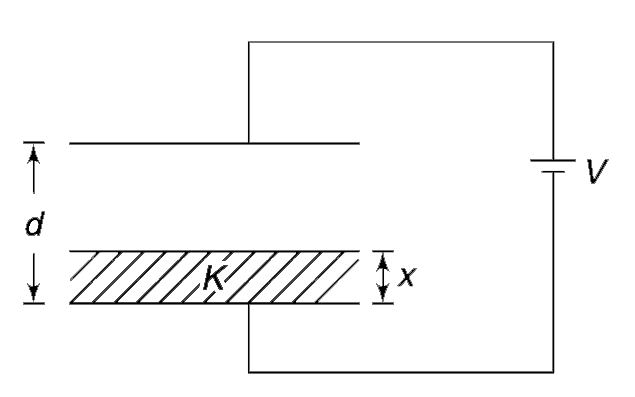
View SolutionWhen a liquid is placed in a closed container, the level of the liquid initially decreases but eventually becomes constant. Give reasons.
View SolutionIf the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
View SolutionA parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be

View SolutionA parallel plate capacitor carries a harge Q. If a dielectric slab with dielectric constant K=2 is dipped between the plates, then
View Solution

