In Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
sin−1(λd)
sin−1(λ2d)
sin−1(λ3d)
sin−1(λ4d)
The correct Answer is:C
I=Imaxcos2(ϕ2)Imax4=Imaxcos2ϕ2
cosϕ2=12
ϕ2=π3
⇒ϕ=2π3=(2πλ)×Δx …(i)
where, Δx=dsinθ
Putting the value of Δx in Eq. (i), we get
sinθ=λ3d
θ=sin−1(λ3d)
Topper's Solved these Questions
Similar Questions
Knowledge Check
In Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
Asin−1(λd)Bsin−1(λ2d)Csin−1(λ3d)Dsin−1(λ4d)In Young's double - slit experiment intensity at a point is (3/4)th of the maximum intensity. The possible angular position of this point is
Asin−1(λ3d)Bsin−1(λ2a)Csin−1(λ6d)Dsin−1(λ4d)In Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
Asin−1(λd)Bsin−1(λ2d)Csin−1(λ3d)Dsin−1(λ4d)
Youngs Double slit experiment | variation of intensity on screen
View SolutionIn young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
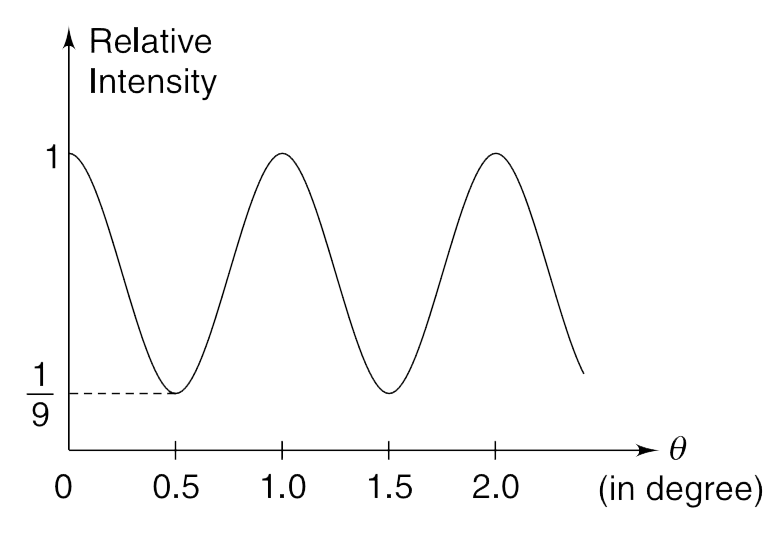
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
View SolutionIn a Young's double slit experiment, the central point on the screen is
View SolutionIn Young's double slit experiment, if the slit widths are in the ratio 1:9, then the ratio of the intensity at minima to that at maxima will be
View Solution

