The ratio of angular momentum L to the atomic dipole moment μi for hydrogen like atoms and ions is
always constant and is equal to the ratio of mass to the charge of electron
always constant and is equal to twice the ratio of mass to the charge of electron to the principal quantum number n?
Proportional to the principal quantum number n
proportional to 1n2
The correct Answer is:A
To find the ratio of angular momentum L to the atomic dipole moment μi for hydrogen-like atoms and ions, we will follow these steps:
Step 1: Understand the Angular Momentum
The angular momentum L of an electron revolving in a circular orbit around the nucleus is given by the formula:
L=mvr
where:
- m is the mass of the electron,
- v is the speed of the electron,
- r is the radius of the orbit.
Step 2: Calculate the Atomic Dipole Moment
The atomic dipole moment μi can be calculated using the formula:
μi=i⋅A
where:
- i is the current,
- A is the area of the orbit.
Step 3: Determine the Current i
The current i due to the revolving electron can be expressed as:
i=qT
where:
- q is the charge of the electron (denoted as e),
- T is the time period for one complete revolution.
The time period T can be calculated as:
T=2πrv
Substituting this into the expression for current, we get:
i=eT=e⋅v2πr
Step 4: Calculate the Area A
The area A for a circular orbit is:
A=πr2
Step 5: Substitute into the Dipole Moment Formula
Now substituting i and A into the dipole moment formula:
μi=(e⋅v2πr)⋅(πr2)=evr2
Step 6: Formulate the Ratio Lμi
Now, we can find the ratio of angular momentum to the dipole moment:
Lμi=mvrevr2=mvr⋅2evr
Here, v and r cancel out:
Lμi=2me
Conclusion
The ratio of angular momentum L to the atomic dipole moment μi for hydrogen-like atoms and ions is:
Lμi=2me
The angular momentum L of an electron revolving in a circular orbit around the nucleus is given by the formula:
L=mvr
where:
- m is the mass of the electron,
- v is the speed of the electron,
- r is the radius of the orbit.
The atomic dipole moment μi can be calculated using the formula:
μi=i⋅A
where:
- i is the current,
- A is the area of the orbit.
The current i due to the revolving electron can be expressed as:
i=qT
where:
- q is the charge of the electron (denoted as e),
- T is the time period for one complete revolution.
T=2πrv
Substituting this into the expression for current, we get:
i=eT=e⋅v2πr
The area A for a circular orbit is:
A=πr2
Now substituting i and A into the dipole moment formula:
μi=(e⋅v2πr)⋅(πr2)=evr2
Now, we can find the ratio of angular momentum to the dipole moment:
Lμi=mvrevr2=mvr⋅2evr
Here, v and r cancel out:
Lμi=2me
The ratio of angular momentum L to the atomic dipole moment μi for hydrogen-like atoms and ions is:
Lμi=2me
Topper's Solved these Questions
Similar Questions
Knowledge Check
The angular momentum of electrons in an atom produces
Amagnetic momentBZEEMAN effectClightDnuclear fissionThe angular momentum of an electron in an atom depends on
AmBlCnDAll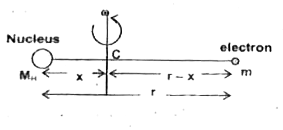
The angular momentum of the atom about the centre of mass will beAmr2ωBm(r−X)2ωC(MH+M)r2ωMHm2DMHmMH+mr2ω
Consider a particle of charge q describing a closed orbit like that of an electron in an atom.The angular momentum of the particle L and the magnetic dipole moment M of the corresponding current loop are related as (m− is the mass of a charged particle)
View SolutionConsider a particle of charge q describing a closed orbit like that of an electron in an atom.The angular momentum of the particle L and the magnetic dipole moment M of the corresponding current loop are related as (m- is the mass of a charged particle)
View SolutionThe angular momentum of elerctro of H-atom is proprtional to :
View SolutionThe angular momentum of electron of H-atom is proportional to :
View SolutionConsider the following parameters with regard to hydrogen like atoms:
(1). Energy of the atom
(2). Radius of electron orbit
(3) Spin of the electron
Which of the above are same for all hydrogen-like atoms and ions in n=1 state?
View Solution
