Question

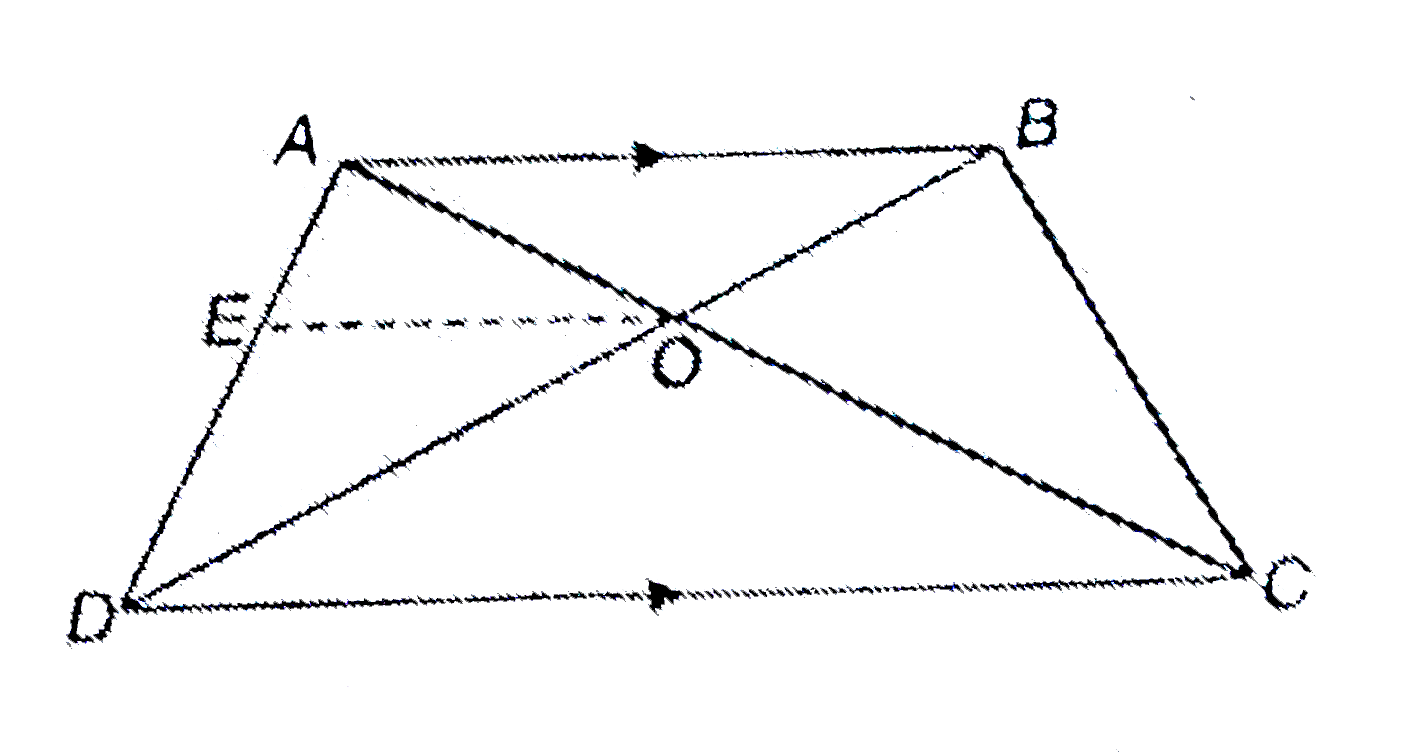
Length of parallel sides AB and CD of a trapezium are respectively 10 cm and 14 cm. If its diagonals AC and BD intersects at O then AO : OC is

Options

A. `5:7`
B. `12:7`
C. `7:5`
D. `7:12`

Answer

A

Explanation

To solve the problem, we need to find the ratio $$AO:OC$$ in the trapezium $$ABCD$$ where $$AB$$ and $$CD$$ are the parallel sides. The lengths of these sides are given as follows:

- $$AB=10\text{cm}$$
- $$CD=14\text{cm}$$

1. Identify the properties of the trapezium:
Since \( AB \) and \( CD \) are parallel sides of the trapezium, we can use the properties of similar triangles formed by the diagonals \( AC \) and \( BD \).

2. Draw the trapezium and label the points:
Let \( O \) be the point where the diagonals \( AC \) and \( BD \) intersect. We have two triangles: \( \triangle AOB \) and \( \triangle DOC \).

3. Use the Angle-Angle (AA) similarity criterion:
Since \( AB \parallel CD \), the angles formed by the diagonals with the parallel sides are equal:
- \( \angle AOB = \angle DOC \) (alternate interior angles)
- \( \angle ABO = \angle CDO \) (alternate interior angles)

Therefore, by the AA criterion, \( \triangle AOB \sim \triangle DOC \).

4. Set up the ratio of corresponding sides:
From the similarity of triangles, we know that the ratios of corresponding sides are equal:
\( \frac{AO}{OC} = \frac{AB}{CD} \)

5. Substitute the lengths of the parallel sides:
We know:
- \( AB = 10 \, \text{cm} \)
- \( CD = 14 \, \text{cm} \)

Thus, we can substitute these values into the ratio:
\( \frac{AO}{OC} = \frac{10}{14} \)

6. Simplify the ratio:
To simplify \( \frac{10}{14} \):
\( \frac{10}{14} = \frac{5}{7} \)

7. Final result:
Therefore, the ratio \( AO : OC \) is:
\( AO : OC = 5 : 7 \)

Conclusion:
The final answer is \( AO : OC = 5 : 7 \).