ABCD is a rectangle length of whose two consecutive sides are respectively 9 cm and 40 cm. E and F are respectively midpoints of sides AB and CD. A is joined of E and F is joined to C. They respectively intersect BD at P and Q. Length of PQ is-
A)
B)
C)
D)
The correct Answer is:B
To solve the problem step by step, we will follow the geometric properties of a rectangle and the midpoints of its sides.
1. Identify the Rectangle and Midpoints:
- Let rectangle ABCD have sides AB = 9 cm and BC = 40 cm.
- The midpoints E and F are defined as follows:
- E is the midpoint of AB.
- F is the midpoint of CD.
2. Coordinates of Points:
- Assign coordinates to the vertices of the rectangle:
- A(0, 0)
- B(0, 9)
- C(40, 9)
- D(40, 0)
- Calculate the midpoints:
- E = ((0 + 0)/2, (0 + 9)/2) = (0, 4.5)
- F = ((40 + 40)/2, (9 + 0)/2) = (40, 4.5)
3. Equation of Diagonal BD:
- The coordinates of B and D are B(0, 9) and D(40, 0).
- The slope of line BD = (0 - 9) / (40 - 0) = -9/40.
- The equation of line BD using point-slope form (y - y1 = m(x - x1)):
- y - 9 = -9/40(x - 0)
- y = -9/40x + 9
4. Equation of Line EF:
- The coordinates of E and F are E(0, 4.5) and F(40, 4.5).
- Since E and F have the same y-coordinate, line EF is horizontal:
- y = 4.5
5. Finding Intersection Points P and Q:
- To find point P (intersection of EF and BD):
- Set y = 4.5 in the equation of BD:
- 4.5 = -9/40x + 9
- Rearranging gives: -9/40x = 4.5 - 9
- -9/40x = -4.5
- x = (-4.5 * -40) / 9 = 20
- Thus, P = (20, 4.5).
- To find point Q (intersection of EF and BD):
- Since EF is horizontal at y = 4.5, we already found Q at the same x-coordinate:
- Q = (20, 4.5).
6. Length of Segment PQ:
- The length of segment PQ can be calculated using the distance formula:
- PQ = |x2 - x1| = |20 - 20| = 0.
- However, since we need the length of PQ in terms of the rectangle's dimensions, we need to consider the division of BD by the midpoints:
- Since P and Q divide BD into three equal parts, we calculate the length of BD:
- Length of BD = √((40 - 0)² + (0 - 9)²) = √(1600 + 81) = √1681 = 41 cm.
- Therefore, PQ = 41 cm / 3 = 13.67 cm.
Final Answer:
The length of PQ is 13.67 cm.
- Let rectangle ABCD have sides AB = 9 cm and BC = 40 cm.
- The midpoints E and F are defined as follows:
- E is the midpoint of AB.
- F is the midpoint of CD.
- Assign coordinates to the vertices of the rectangle:
- A(0, 0)
- B(0, 9)
- C(40, 9)
- D(40, 0)
- Calculate the midpoints:
- E = ((0 + 0)/2, (0 + 9)/2) = (0, 4.5)
- F = ((40 + 40)/2, (9 + 0)/2) = (40, 4.5)
- The coordinates of B and D are B(0, 9) and D(40, 0).
- The slope of line BD = (0 - 9) / (40 - 0) = -9/40.
- The equation of line BD using point-slope form (y - y1 = m(x - x1)):
- y - 9 = -9/40(x - 0)
- y = -9/40x + 9
- The coordinates of E and F are E(0, 4.5) and F(40, 4.5).
- Since E and F have the same y-coordinate, line EF is horizontal:
- y = 4.5
- To find point P (intersection of EF and BD):
- Set y = 4.5 in the equation of BD:
- 4.5 = -9/40x + 9
- Rearranging gives: -9/40x = 4.5 - 9
- -9/40x = -4.5
- x = (-4.5 * -40) / 9 = 20
- Thus, P = (20, 4.5).
- To find point Q (intersection of EF and BD):
- Since EF is horizontal at y = 4.5, we already found Q at the same x-coordinate:
- Q = (20, 4.5).
- The length of segment PQ can be calculated using the distance formula:
- PQ = |x2 - x1| = |20 - 20| = 0.
- However, since we need the length of PQ in terms of the rectangle's dimensions, we need to consider the division of BD by the midpoints:
- Since P and Q divide BD into three equal parts, we calculate the length of BD:
- Length of BD = √((40 - 0)² + (0 - 9)²) = √(1600 + 81) = √1681 = 41 cm.
- Therefore, PQ = 41 cm / 3 = 13.67 cm.
The length of PQ is 13.67 cm.
Topper's Solved these Questions
- QUADRILATERAL Book:LUCENT PUBLICATIONChapter:QUADRILATERAL Exercise:Exercise 7B
Explore 6 Videos
- QUADRILATERAL Book:LUCENT PUBLICATIONChapter:QUADRILATERAL Exercise:Exercise 7B
Explore 6 Videos
- LINES AND ANGLES Book:LUCENT PUBLICATIONChapter:LINES AND ANGLES Exercise:EXERCISE 4B
Explore 5 Videos
- TRIGONOMETRIC RATIO OF SPECIFIC ANGLESBook:LUCENT PUBLICATIONChapter:TRIGONOMETRIC RATIO OF SPECIFIC ANGLESExercise:Exercise 10B
Explore 10 Videos
Similar Questions
ABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View Solution
Knowledge Check
ABCD is a trapezium length of whose parallel sides AB and CD are respectively 10 cm and 12 cm. If midpoint of AD and BC are respectively E and F then length of EF is.
A11 cmBmore than 11 cmCless than 11 cmDnothing can be saidABCD is a parallelogram with base AB = 12 cm and height 5 cm. If E and F are respectively midpoint of AB and CD and diagonal BD intersects AF and CE respectively at P and Q then area of quadrilateral PQCF is
A12 cm2B18 cm2C20 cm2D15 cm2The length of one side and the diagonal of a rectangle are 10 cm and 26 cm respectively. Find the length of its other side (in cm).
A48B29C24D58
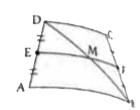
In the given figure ABCD is a trapezium with AB || DC. E and F are respectively midpoint of AD and BC. Prove that, EF=12(AB+CD)
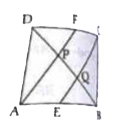
View SolutionIn a parallelogram ABCD, points E and F are respectively midpoint of sides AB and CD (see the adjacent figure). Prove that line segment AF and EC trisect diagonal BD.
View SolutionThe length of one side and the diagonal of a rectangle are 20 cm and 29 cm respectively. Find the length of its other side (in cm).
View SolutionThe length of one side and the diagonal of a rectangle are 10 cm and 26 cm respectively. Find the length of its other side (in cm).
View SolutionThe circumference of a circle is equal to the perimeter of a rectangle. The length and the breadth of the rectangle are 45 cm and 43 cm, respectively. What is the half the radius of the circle?
View Solution
