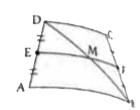
ABCD is a trapezium length of whose parallel sides AB and CD are respectively 10 cm and 12 cm. If midpoint of AD and BC are respectively E and F then length of EF is.
11 cm
more than 11 cm
less than 11 cm
nothing can be said
The correct Answer is:A
To find the length of EF in trapezium ABCD, where AB and CD are the parallel sides, we can follow these steps:
Step 1: Identify the lengths of the parallel sides
Given:
- Length of AB = 10 cm
- Length of CD = 12 cm
Step 2: Use the formula for the length of the line segment joining the midpoints of the non-parallel sides
The length of EF, which connects the midpoints E and F of the non-parallel sides AD and BC respectively, can be calculated using the formula:
EF=12(AB+CD)
Step 3: Substitute the values into the formula
Now, substitute the lengths of AB and CD into the formula:
EF=12(10cm+12cm)
Step 4: Calculate the sum of the lengths
Calculate the sum:
10cm+12cm=22cm
Step 5: Divide by 2 to find EF
Now, divide the sum by 2:
EF=12×22cm=11cm
Final Answer
Thus, the length of EF is:
11cm
---
Given:
- Length of AB = 10 cm
- Length of CD = 12 cm
The length of EF, which connects the midpoints E and F of the non-parallel sides AD and BC respectively, can be calculated using the formula:
EF=12(AB+CD)
Now, substitute the lengths of AB and CD into the formula:
EF=12(10cm+12cm)
Calculate the sum:
10cm+12cm=22cm
Now, divide the sum by 2:
EF=12×22cm=11cm
Thus, the length of EF is:
11cm
Topper's Solved these Questions
- QUADRILATERAL BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B
6 Videos
- QUADRILATERAL BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B
6 Videos
- LINES AND ANGLES BOOK - LUCENT PUBLICATIONCHAPTER - LINES AND ANGLES EXERCISE - EXERCISE 4B
5 Videos
- TRIGONOMETRIC RATIO OF SPECIFIC ANGLESBOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B
10 Videos
Similar Questions
Knowledge Check
Length of parallel sides AB and CD of a trapezium are respectively 10 cm and 14 cm. If its diagonals AC and BD intersects at O then AO : OC is
A5:7B12:7C7:5D7:12ABCD is a rectangle length of whose two consecutive sides are respectively 9 cm and 40 cm. E and F are respectively midpoints of sides AB and CD. A is joined of E and F is joined to C. They respectively intersect BD at P and Q. Length of PQ is-
AA)313cmBB)413cmCC)493cmDD)473cmABCD is a trapezium of sides in which BC || AB & AB=9cm, BC=12cm, CD=15cm & DA=20cm. Find the sum of square of its diagonal.
A638B786C838D814
In the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = 911 ar(EFCD).
View SolutionABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
View SolutionABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :

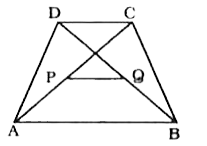
View SolutionIn trapezium ABCD,AB∣∣CDwith AB=24cm.andCD=16cm. P and Q are mid-points of the diagonals AC and BD respectively. Find the length of PQ.
View Solution