In the adjacent figure ABCD is a quadrilateral. AB, DC are parallel and AD, BC are parallel. ADC is a right angle. If perimeter of ΔABE is 6 unit, then what is the area of the quadrilateral ?
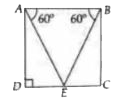
2√3 sq. unit
4 sq. unit
3 sq.unit
4√3 sq. unit
The correct Answer is:A
Step by step video, text & image solution for In the adjacent figure ABCD is a quadrilateral. AB, DC are parallel and AD, BC are parallel. ADC is a right angle. If perimeter of DeltaABE is 6 unit, then what is the area of the quadrilateral ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERAL Book:LUCENT PUBLICATIONChapter:QUADRILATERAL Exercise:Exercise 7B
Explore 6 Videos
- QUADRILATERAL Book:LUCENT PUBLICATIONChapter:QUADRILATERAL Exercise:Exercise 7B
Explore 6 Videos
- LINES AND ANGLES Book:LUCENT PUBLICATIONChapter:LINES AND ANGLES Exercise:EXERCISE 4B
Explore 5 Videos
- TRIGONOMETRIC RATIO OF SPECIFIC ANGLESBook:LUCENT PUBLICATIONChapter:TRIGONOMETRIC RATIO OF SPECIFIC ANGLESExercise:Exercise 10B
Explore 10 Videos
Similar Questions
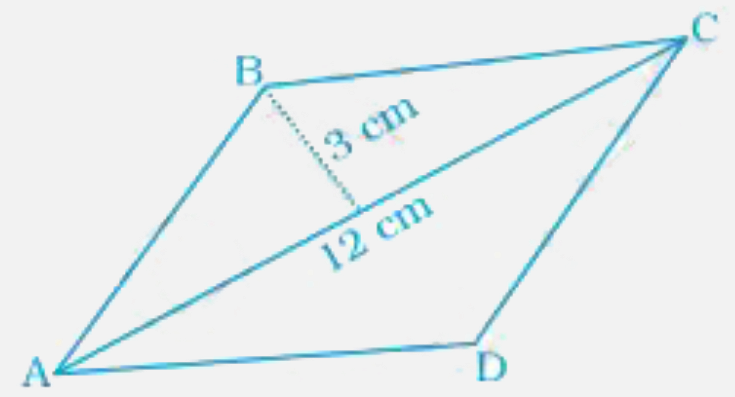
The figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View SolutionThe given figure shows a quadrilateral ABCD.
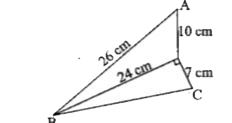
What is the area of quadrilateral ABCD?
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠C=∠D

View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionABCD is a quadrilateral in which AB=CD and AD=BC. show that it is a parallelogram.
View SolutionIn the given figure ABCD is, ABCD is a quadrilateral in which AB∣∣DC and AD∣∣BC prove that ANGLEADC=ANGLEABC.

View SolutionIn quadrilateral ABCD, AB ||CD and AD= BC, prove that ∠A=∠B.
View SolutionABCD is a quadrilateral and let AB=→a, AD=→b, AC=m→a+n→b then the area of the quadrilateral is
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View Solution
