The relation between radius (r) and diameter (d) is___
d=2xr
d=r/2
d=r/3
d=3r
The correct Answer is:a
To find the relation between the radius (r) and diameter (d) of a circle, we can follow these steps:
1. Understand the Definitions:
- The diameter (d) of a circle is defined as the longest distance across the circle, passing through the center. It connects two points on the circle.
- The radius (r) of a circle is defined as the distance from the center of the circle to any point on its circumference.
2. Visualize the Circle:
- Imagine a circle with a center point. Draw a line from the center to the edge of the circle. This line represents the radius (r).
- Now, draw a line that passes through the center and touches both ends of the circle. This line represents the diameter (d).
3. Relate Radius to Diameter:
- If you consider the diameter, it is made up of two radii. That is, if you start from one edge of the circle, go to the center (which is one radius), and then from the center to the other edge (which is another radius).
- Therefore, the diameter can be expressed as the sum of two radii:
d=r+r
4. Simplify the Equation:
- Since r+r is the same as 2r, we can rewrite the equation as:
d=2r
5. Conclusion:
- The relation between the radius and diameter of a circle is:
d=2r
- The diameter (d) of a circle is defined as the longest distance across the circle, passing through the center. It connects two points on the circle.
- The radius (r) of a circle is defined as the distance from the center of the circle to any point on its circumference.
- Imagine a circle with a center point. Draw a line from the center to the edge of the circle. This line represents the radius (r).
- Now, draw a line that passes through the center and touches both ends of the circle. This line represents the diameter (d).
- If you consider the diameter, it is made up of two radii. That is, if you start from one edge of the circle, go to the center (which is one radius), and then from the center to the other edge (which is another radius).
- Therefore, the diameter can be expressed as the sum of two radii:
d=r+r
- Since r+r is the same as 2r, we can rewrite the equation as:
d=2r
- The relation between the radius and diameter of a circle is:
d=2r
Topper's Solved these Questions
- BASIC GEOMETRICAL IDEASBook:MTG IIT JEE FOUNDATIONChapter:BASIC GEOMETRICAL IDEASExercise:EXERCISE(MCQ)LEVEL-2
Explore 10 Videos
- BASIC GEOMETRICAL IDEASBook:MTG IIT JEE FOUNDATIONChapter:BASIC GEOMETRICAL IDEASExercise:MATCH THE FOLLOWING
Explore 2 Videos
- BASIC GEOMETRICAL IDEASBook:MTG IIT JEE FOUNDATIONChapter:BASIC GEOMETRICAL IDEASExercise:NCERT SECTION(EXERCISE 4.6)
Explore 20 Videos
- ALGEBRABook:MTG IIT JEE FOUNDATIONChapter:ALGEBRAExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
- DATA HANDLING Book:MTG IIT JEE FOUNDATIONChapter:DATA HANDLING Exercise:Olympiad/HOTS Corner
Explore 10 Videos
Similar Questions
Knowledge Check
The relation between atomic radius (r ) and the edge (a) of the unit cell are given below. Which is correctly matched.
ASimple cubic r=a2BFace centred r=0.3535aCBody centred r = 0.433aDAll of the above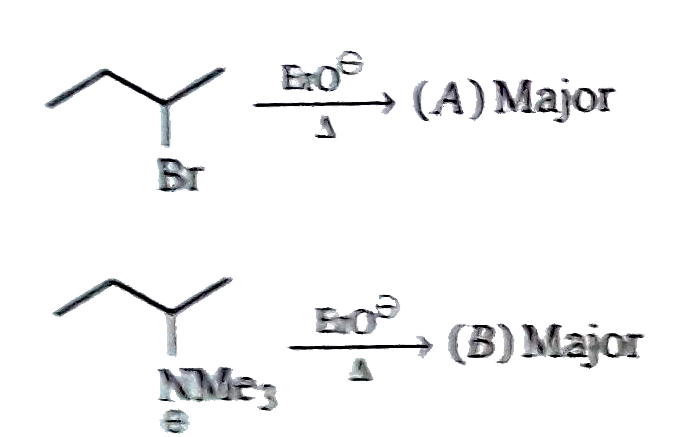
relation between (A) an d(B) is :AGgtIBPostitional isomerCEnanttiomerDChain isomerThe relation between atomic radius ( r ) and edge length ( a ) a face - centred cubic cell is
Ar=a2Br=a2√2Cr=a√34D√2a2
Relation between μrandχ will be
View SolutionThe relation between radius of third orbit r3 and radius of first orbit r1 in hydrogen atom would be
View SolutionIn a discrete series , the relation between s.d.s and range r is
View Solution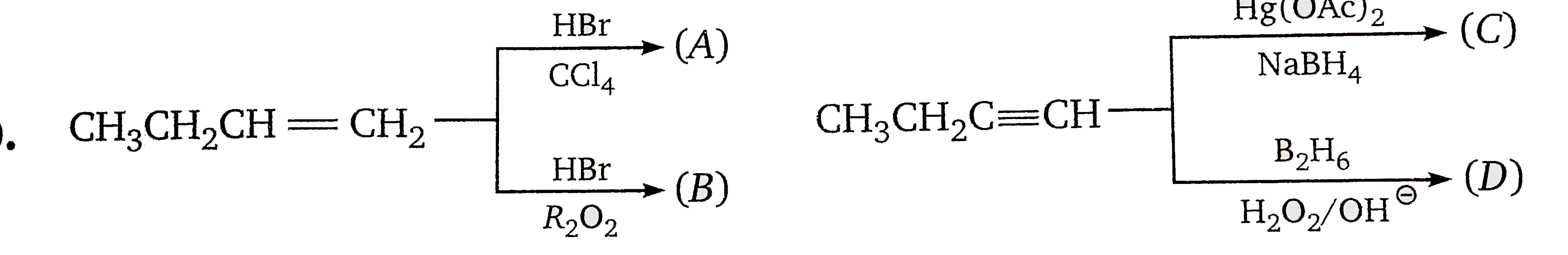
Relation between A and B, C and D are:
View SolutionA particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
View Solution
