The relation between atomic radius (r ) and the edge (a) of the unit cell are given below. Which is correctly matched.
Simple cubic r=a2
Face centred r=0.3535a
Body centred r = 0.433a
All of the above
The correct Answer is:D
To determine the correct relationships between atomic radius (r) and the edge length (a) of the unit cell for different types of cubic structures, we will analyze the simple cubic, face-centered cubic (FCC), and body-centered cubic (BCC) unit cells step by step.
Step 1: Simple Cubic Unit Cell
1. Understanding the Structure: In a simple cubic unit cell, atoms are located only at the corners of the cube.
2. Edge Length and Atomic Radius: The edge length (a) is equal to twice the atomic radius (r) because the atoms at the corners touch each other along the edge.
a=2r⟹r=a2
3. Conclusion for Simple Cubic: The relationship for the simple cubic unit cell is correctly given as r=a2.
Step 2: Face-Centered Cubic Unit Cell
1. Understanding the Structure: In a face-centered cubic unit cell, atoms are located at each corner and at the center of each face of the cube.
2. Calculating the Face Diagonal: The face diagonal can be calculated using Pythagoras' theorem. The length of the face diagonal (d) is given by:
d=a√2
3. Atoms Along the Face Diagonal: Along the face diagonal, there are 4 atomic radii (2 from each corner atom and 1 from the face-centered atom):
d=4r
4. Setting the Equations Equal: Set the two expressions for the face diagonal equal:
a√2=4r⟹r=a√24=a2√2≈0.3535a
5. Conclusion for Face-Centered Cubic: The relationship for the face-centered cubic unit cell is correctly given as r=a√24.
Step 3: Body-Centered Cubic Unit Cell
1. Understanding the Structure: In a body-centered cubic unit cell, atoms are located at each corner and one atom at the center of the cube.
2. Calculating the Body Diagonal: The body diagonal can be calculated as:
d=a√3
3. Atoms Along the Body Diagonal: Along the body diagonal, there are 4 atomic radii (1 from the center atom and 1 from each corner atom):
d=4r
4. Setting the Equations Equal: Set the two expressions for the body diagonal equal:
a√3=4r⟹r=a√34≈0.433a
5. Conclusion for Body-Centered Cubic: The relationship for the body-centered cubic unit cell is correctly given as r=a√34.
Final Summary of Relationships
- Simple Cubic: r=a2
- Face-Centered Cubic: r=a√24≈0.3535a
- Body-Centered Cubic: r=a√34≈0.433a
1. Understanding the Structure: In a simple cubic unit cell, atoms are located only at the corners of the cube.
2. Edge Length and Atomic Radius: The edge length (a) is equal to twice the atomic radius (r) because the atoms at the corners touch each other along the edge.
a=2r⟹r=a2
3. Conclusion for Simple Cubic: The relationship for the simple cubic unit cell is correctly given as r=a2.
1. Understanding the Structure: In a face-centered cubic unit cell, atoms are located at each corner and at the center of each face of the cube.
2. Calculating the Face Diagonal: The face diagonal can be calculated using Pythagoras' theorem. The length of the face diagonal (d) is given by:
d=a√2
3. Atoms Along the Face Diagonal: Along the face diagonal, there are 4 atomic radii (2 from each corner atom and 1 from the face-centered atom):
d=4r
4. Setting the Equations Equal: Set the two expressions for the face diagonal equal:
a√2=4r⟹r=a√24=a2√2≈0.3535a
5. Conclusion for Face-Centered Cubic: The relationship for the face-centered cubic unit cell is correctly given as r=a√24.
1. Understanding the Structure: In a body-centered cubic unit cell, atoms are located at each corner and one atom at the center of the cube.
2. Calculating the Body Diagonal: The body diagonal can be calculated as:
d=a√3
3. Atoms Along the Body Diagonal: Along the body diagonal, there are 4 atomic radii (1 from the center atom and 1 from each corner atom):
d=4r
4. Setting the Equations Equal: Set the two expressions for the body diagonal equal:
a√3=4r⟹r=a√34≈0.433a
5. Conclusion for Body-Centered Cubic: The relationship for the body-centered cubic unit cell is correctly given as r=a√34.
- Simple Cubic: r=a2
- Face-Centered Cubic: r=a√24≈0.3535a
- Body-Centered Cubic: r=a√34≈0.433a
Topper's Solved these Questions
- SOLID STATEBook:FIITJEEChapter:SOLID STATEExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II
Explore 25 Videos
- SOLID STATEBook:FIITJEEChapter:SOLID STATEExercise:(REASONING TYPE QUESTIONS)
Explore 1 Video
- SOLID STATEBook:FIITJEEChapter:SOLID STATEExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II
Explore 15 Videos
- QUALITATIVE ANALYSIS Book:FIITJEEChapter:QUALITATIVE ANALYSIS Exercise:Single interger answer type
Explore 3 Videos
- STOICHIOMETRY AND BALANCING REDOX REACTION Book:FIITJEEChapter:STOICHIOMETRY AND BALANCING REDOX REACTION Exercise:SINGLE INTEGER ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
Express the relation between atomic radius (r) and edge length (a) in b.c.c. unit cell.
View SolutionConsider the parallelotrams shown in the figure below representing two-dimensional cells.
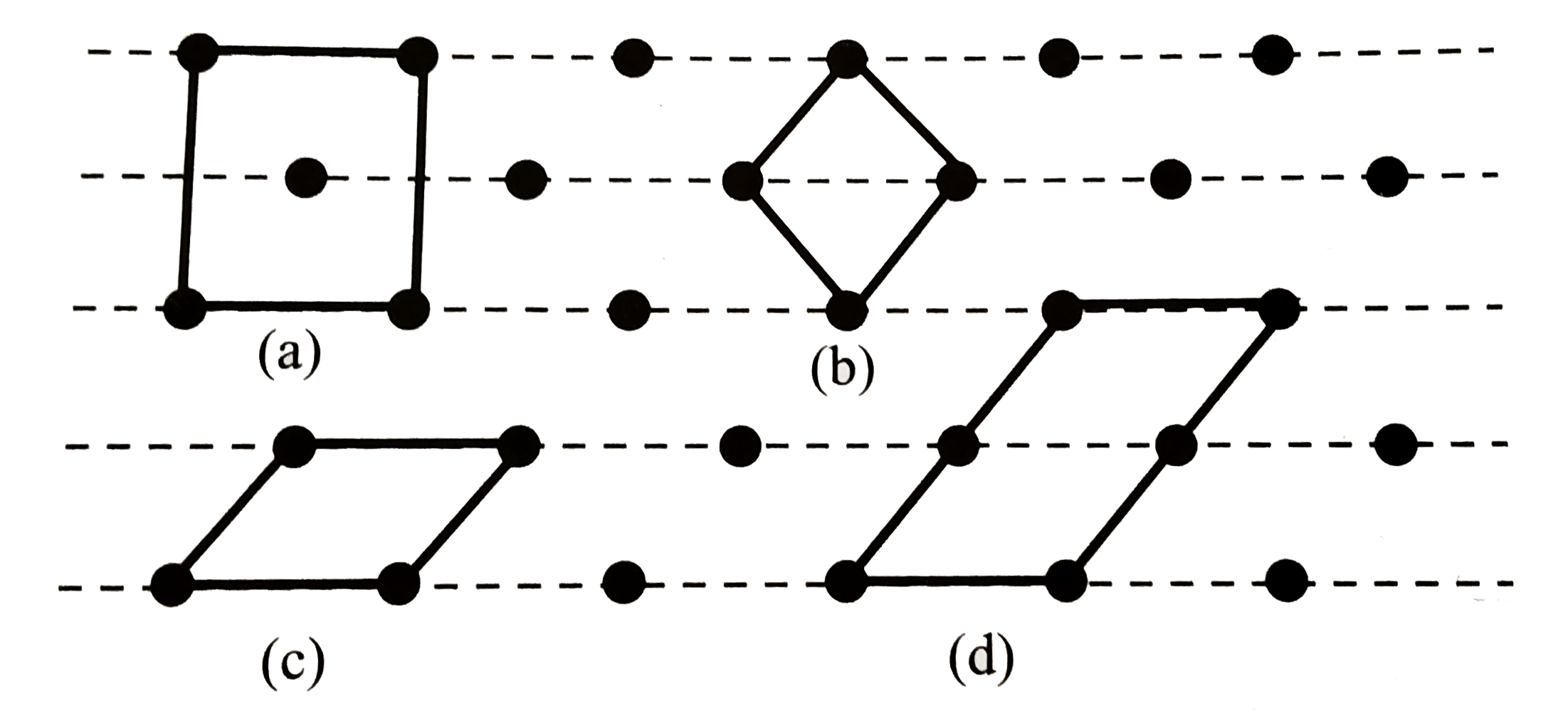
a. Which of these are primitive and which are multiple unit cells? Are any of these orthogonal?
c. What is the relation between the radius of circle and the length of parallelogram for the unit cell shown in the figure below (space filling diagram)?
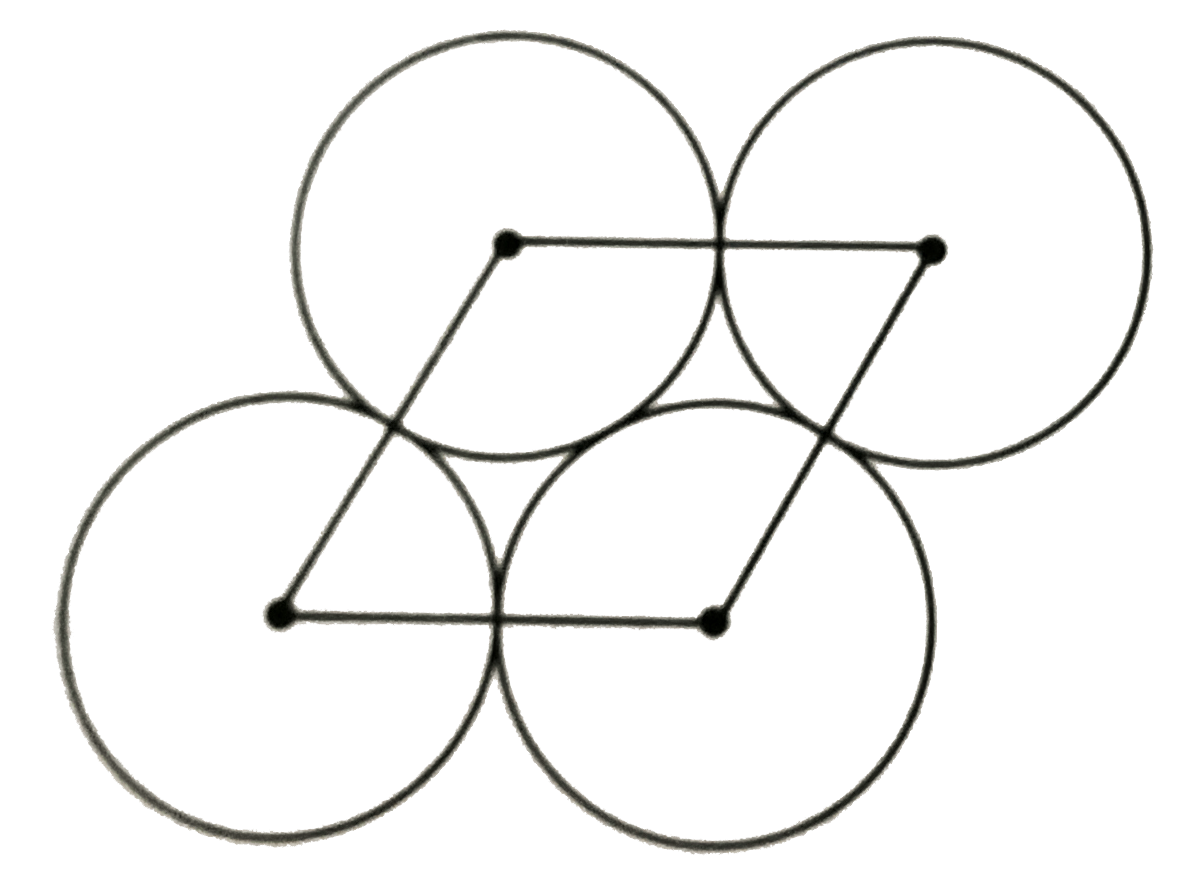
d. How many nearest neighbour circles does a given circle have in the second figure abov?
e. What is the radius of the triangular hole shown in the second figure above?
f. What is the packing fraction of the unit cell in the second figure above?
View Solution
Knowledge Check
The relation between atomic radius ( r ) and edge length ( a ) a face - centred cubic cell is
Ar=a2Br=a2√2Cr=a√34D√2a2Which one of the pairs given below is NOT correctly matched ?
AEquality below law Guaranteed to both citizens and non-citizensBAltering the name of a State Power of a State LegislatureCCreating a new State Power of ParliamentDEquality of opportunity in Public employment Guaranteed only to Indian CitizensThe relation between atomic radius and edge length 'a' of a body centred cubic unit cell :
Ar=a/2Br=√a/2Cr=√34aDr=3a2
Which of the following units is correctly matched?
View SolutionCalculate the radius of Xe atom , If the edge of the unit cell (FCC) is 620 pm.
View SolutionIn a close packed centred cubic lattice of potassium the corrcet relation between the atomic radius (r) of potassium and the edge length (a) of the cube is
View SolutionThe neon atoms has a radius of 160pm. What is the edge of the unit cell of a face centered structure of neon?
View SolutionThe correct relation for radius of atom and edge length in case of FCC arragement is
View Solution

