Consider the parallelotrams shown in the figure below representing two-dimensional cells.
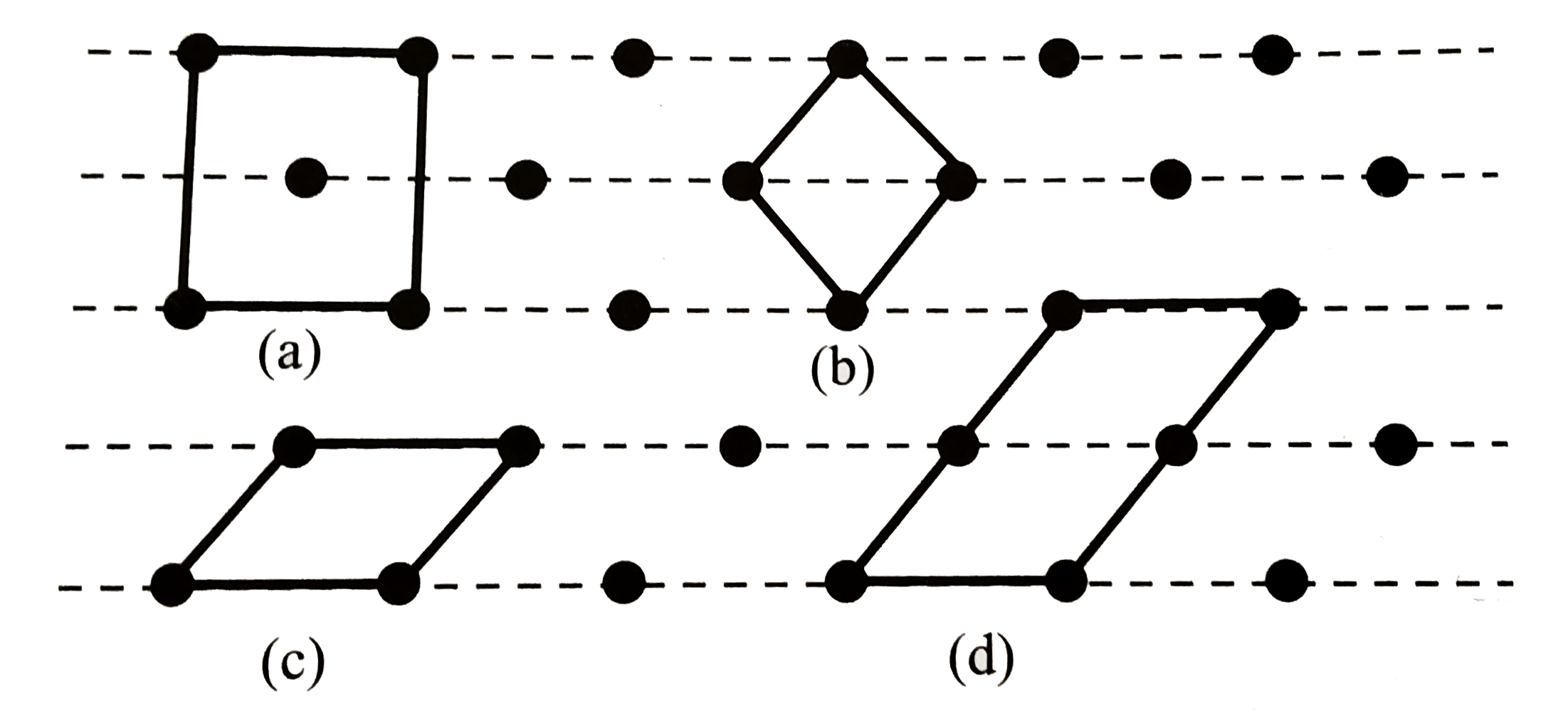
$Consider the parallelotrams shown in the figure below representing two-dimensional cells. a. Which of these are primitive and which are multiple unit cells? Are any of these orthogonal? c. What is the relation between the radius of circle and the length of parallelogram for the unit cell shown in the figure below (space filling diagram)? d. How many nearest neighbour circles does a given circle have in the second figure abov? e. What is the radius of the triangular hole shown in the second figure above? f. What is the packing fraction of the unit cell in the second figure above?$
a. Which of these are primitive and which are multiple unit cells? Are any of these orthogonal?
c. What is the relation between the radius of circle and the length of parallelogram for the unit cell shown in the figure below (space filling diagram)?

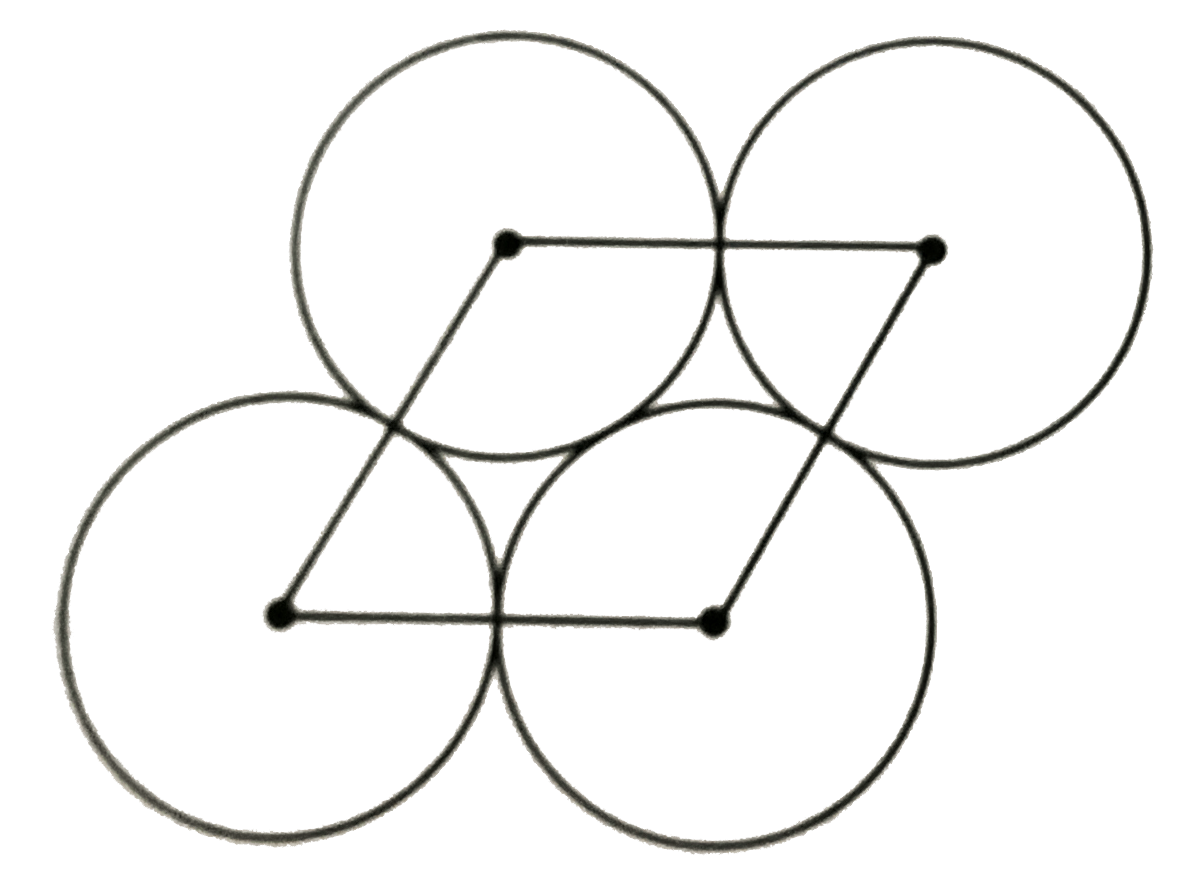
d. How many nearest neighbour circles does a given circle have in the second figure abov?
e. What is the radius of the triangular hole shown in the second figure above?
f. What is the packing fraction of the unit cell in the second figure above?

Video Solution

Text Solution

Verified by Experts

a. Primitive unit cells are $(b)$ and $(c)$ , because the only point contained in the unit cell are at the corners of the parallelograms.
Units cell $(a)$ and $(d)$ are multiple unit cells because there are points in the unit cells in addition to the corners of the parallelogram.
Unit cell $(a)$ is an orthogonal unit cell because it contains angles of $90^{\circ}$ .
b. The unit cell content $(Z)$ is the total number of atoms contained within the unit cell. From the second figure, only part of each circle at each corner is contained within the parallelogram unit cell.
Each circle is touching $4$ other circles, so share of each circle is $\frac{1}{4} \Rightarrow Z = \frac{1}{4} \times 4 = 1$ .
c. $a = 2 R$ , where $a$ is the length of the side of parallelogram and $R$ is the radius of circle.
d. The crystal coordination number $(C N)$ is the number of nearest neighbour around a given atom, ion, or molecule in the crystal.
From the first figure (i), each atom (except the "surface" atom) is touching $6$ other atoms, so $C N = 6$ .
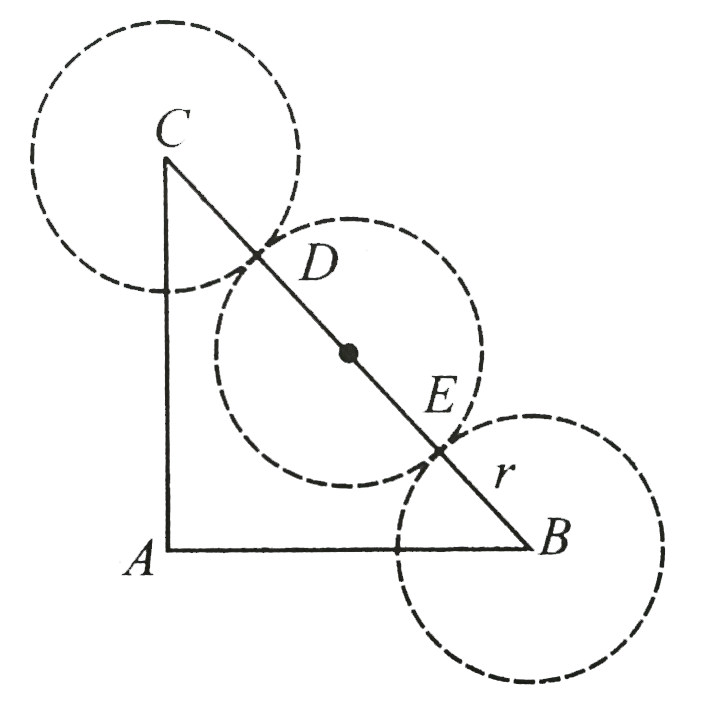
e.
Let $R$ is the radius of larger circle and $r$ is the radius of the triangular hole:

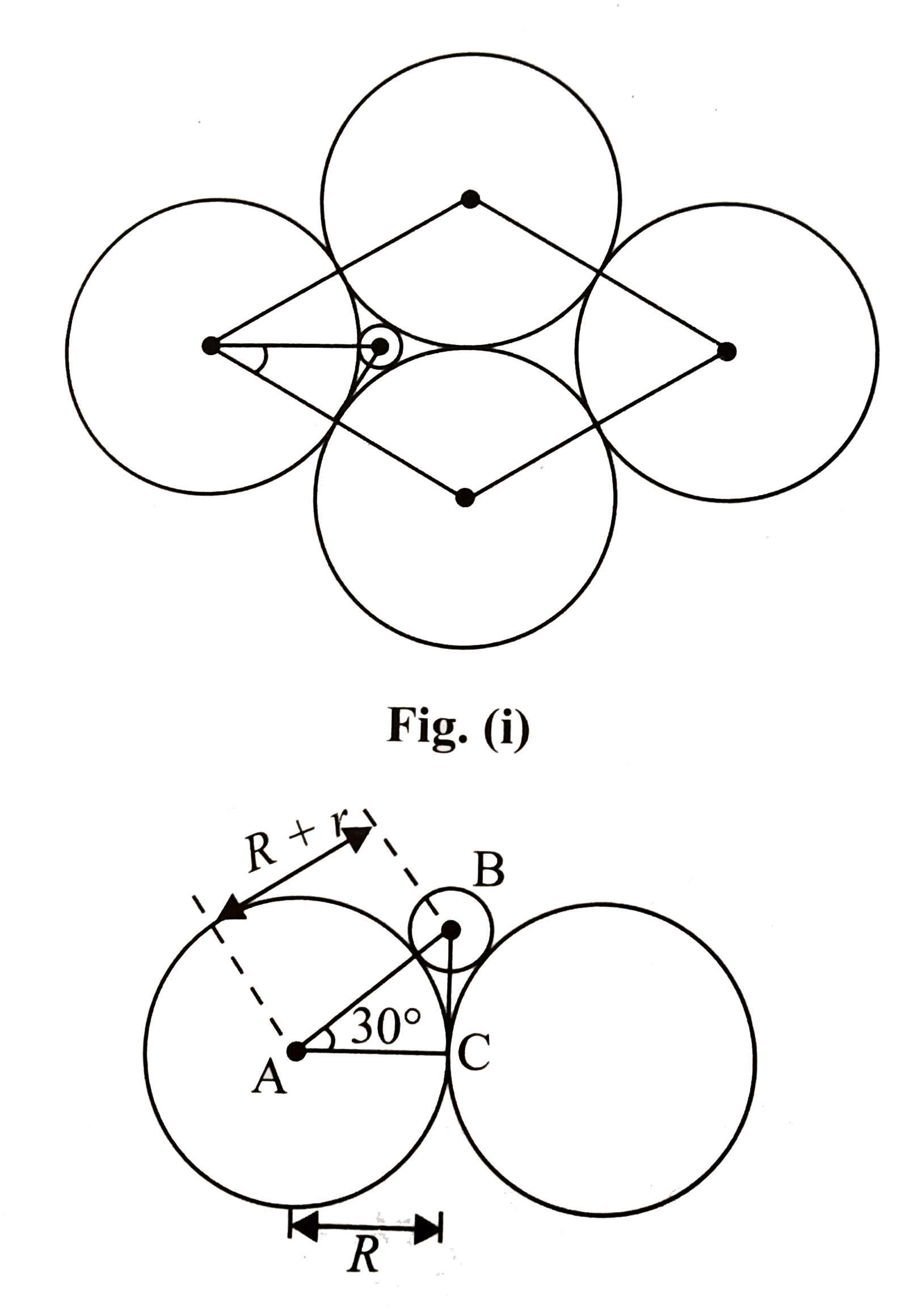
In $Δ A B C, {cos 30}^{\circ} = \frac{Base}{Hypotenuse} = \frac{A C}{A B} = \frac{R}{R + r}$ ,
$\Rightarrow (R + r) {cos}^{30}^(\circ) = R$ .
$\Rightarrow r = (\frac{2}{\sqrt{3}} - 1) R$
f. Packing fraction $= \frac{Area occupied by circles}{Area of unit cell}$
Since $Z = 1$ , area of circle $= π R^{2}$
Area of parallelogram $= 2 \sqrt{3} R^{2}$ ,
$∴ P F = \frac{Z \times π R^{2}}{2 \sqrt{3} R^{2}} = \frac{π}{2 \sqrt{3}} = 0.907$ ,

Updated on:21/07/2023

Stracture of unit cell is described in the given figure packing fraction of the unit cell is?

A $0.521$
B $0.907$
C $0.093$
D $0.745$
The packing efficiency of the 2D square unit cell shown below is

A $39.27 %$
B $68.02 %$
C $74.05 %$
D $78.54 %$
The relation between atomic radius (r ) and the edge (a) of the unit cell are given below. Which is correctly matched.
ASimple cubic $r = \frac{a}{2}$
BFace centred $r = 0.3535 a$
CBody centred r = 0.433a
DAll of the above