The number of arcs made by a chord on a circle is___
3
2
1
4
The correct Answer is:b
To determine the number of arcs made by a chord on a circle, follow these steps:
1. Understand the Definition of a Chord:
A chord is a straight line segment whose endpoints lie on the circumference of the circle. For example, let's denote the endpoints of the chord as point A and point B.
2. Draw the Circle and the Chord:
Start by drawing a circle. Then, draw a chord connecting points A and B on the circle's boundary.
3. Identify the Arcs:
When a chord is drawn, it divides the circle into two distinct parts. Each part is known as an arc.
4. Count the Arcs:
The chord AB creates two arcs:
- The arc that goes from point A to point B in one direction (let's call it Arc AB).
- The arc that goes from point A to point B in the opposite direction (let's call it Arc BA).
5. Conclusion:
Therefore, the number of arcs made by a chord on a circle is 2.
Final Answer:
The number of arcs made by a chord on a circle is 2.
---
A chord is a straight line segment whose endpoints lie on the circumference of the circle. For example, let's denote the endpoints of the chord as point A and point B.
Start by drawing a circle. Then, draw a chord connecting points A and B on the circle's boundary.
When a chord is drawn, it divides the circle into two distinct parts. Each part is known as an arc.
The chord AB creates two arcs:
- The arc that goes from point A to point B in one direction (let's call it Arc AB).
- The arc that goes from point A to point B in the opposite direction (let's call it Arc BA).
Therefore, the number of arcs made by a chord on a circle is 2.
The number of arcs made by a chord on a circle is 2.
Topper's Solved these Questions
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - EXERCISE(MCQ)LEVEL-2
10 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - MATCH THE FOLLOWING
2 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - NCERT SECTION(EXERCISE 4.6)
20 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- DATA HANDLING BOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Olympiad/HOTS Corner
10 Videos
Similar Questions
Knowledge Check
The region enclosed by an arc and a chord of a circle is called .............. of the circle.
AsegmentBquadrantCsectorDarea
Write True or False: Give reasons for your answers.(i) Line segment joining the centre to any point on the circle is a radius of the circle.(ii) A circle has only finite number of equal chords.(iii) If a circle is divided into three equal arcs, each is a major arc.(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.(v) Sector is the region between the chord and its corresponding arc.(vi) A circle is a plane figure.
View SolutionWrite the truth value (T/F) of the following with suitable reasons: A circle is a plane figure. Line segment joining the centre to any point on the circle is a radius of the circle. If a circle is divided into three equal arcs each is a major arc. A circle has only finite number of equal chords. A chord of a circle, which is twice as long is its radius is a diameter of the circle. Sector is the region between the chord and its corresponding arc. The degree measure of an arc is the complement of the central angle containing the arc. The degree measure of a semi-circle is 1800
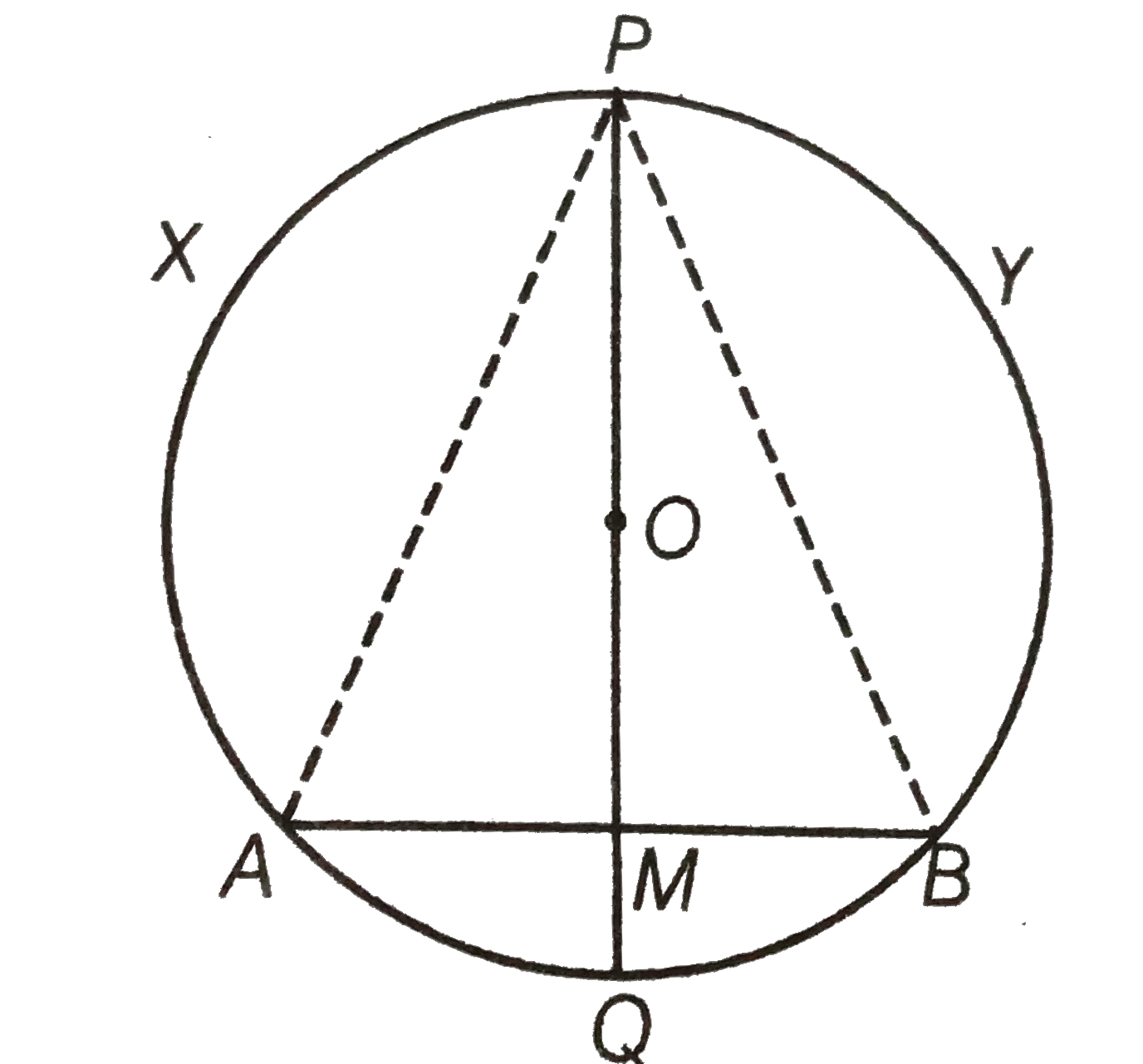
View SolutionIf the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA≅arc PYB.
View SolutionAngle made by a longer chord of circle at its centre is 180∘.
View SolutionAngle made by a longer chord of circle at its centre is 180∘.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View Solution
