If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA≅arc PYB.

Let AB be a chord of a circle having centre at OPQ be the perpendicular bisector of the chord AB, which intersects at M and it always passes through O.

To prove arc PXA≅arc PYB
Construction Join AP and BP.
Proof in ΔAPMandΔBPM,
AM=MB [∵ PM bisects AB]
∠PMA=∠PMB[∵PM⊥AB]
PM=PM [common side]
∴ΔAPM≅ΔBPM [by SAS congruence rule]
∴ PA=PB [by CPCT]
⇒arc PXA≅arc PYB
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLARChapter:CIRCLESExercise:Exercise 10.4
Explore 2 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLARChapter:Areas of Parallelograms and TrianglesExercise:Areas Of Parallelograms And Triangles
Explore 34 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLARChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
Similar Questions
Knowledge Check
The number of arcs made by a chord on a circle is___
A3B2C1D4Chord PQ is the perpendicular bisector of radius OA of circle with centre O (A is a point on the edge of the circle). If the length of Arc PAQ=2π3 . What is the length of chord PQ?
A2B√3C2√3D1
Prove that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
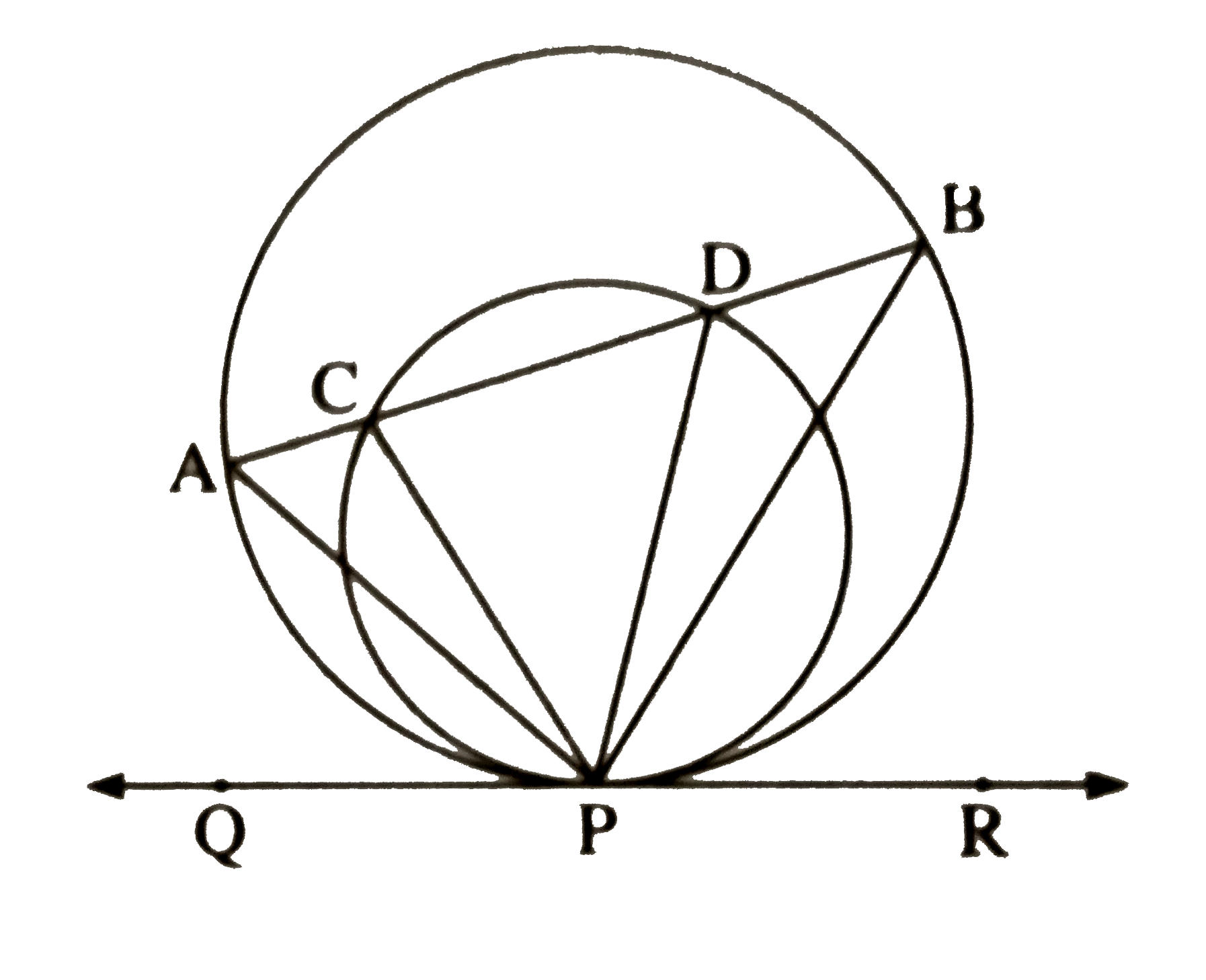
View SolutionIn the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
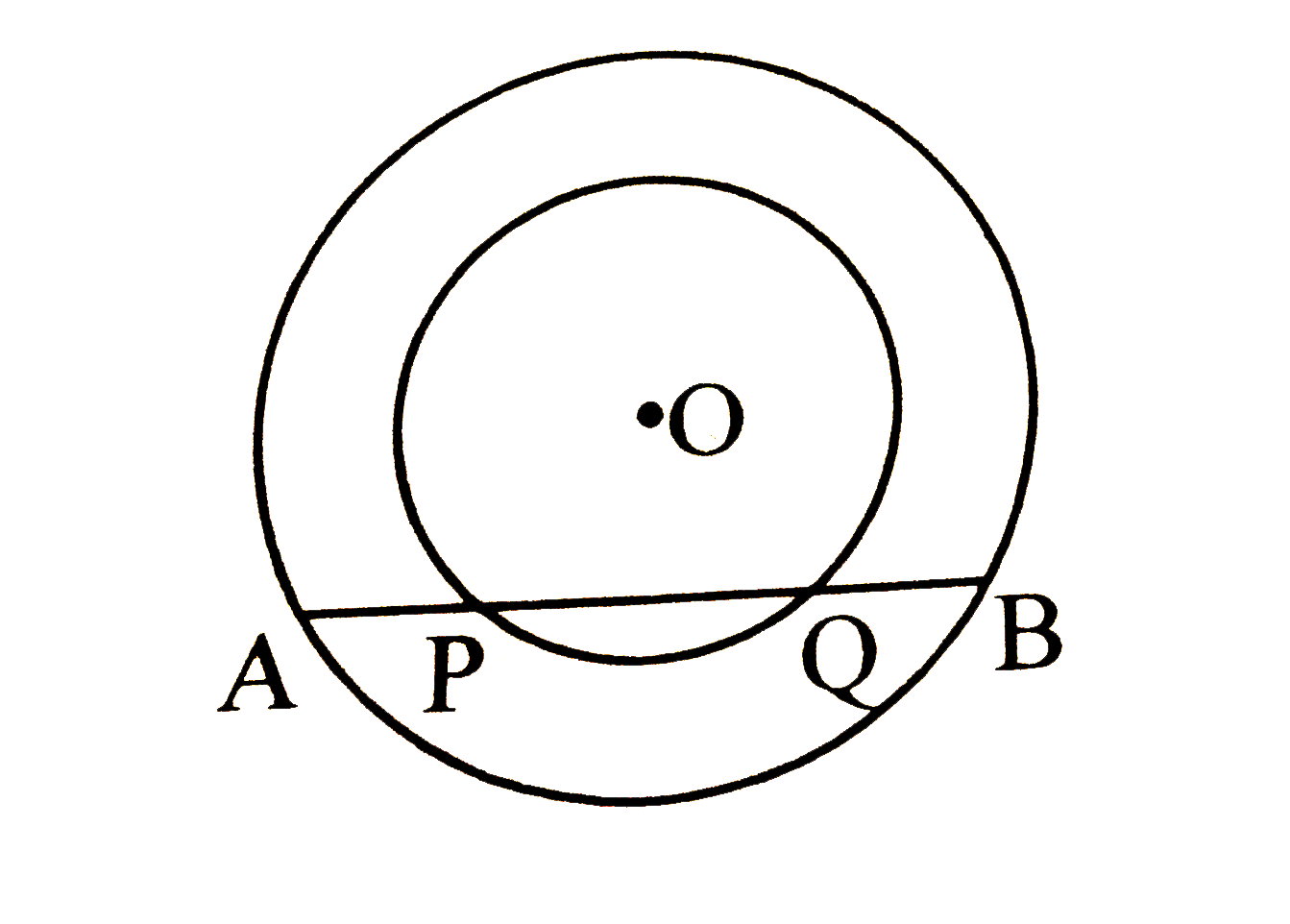
View SolutionIn the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q . Show that AP = BQ.
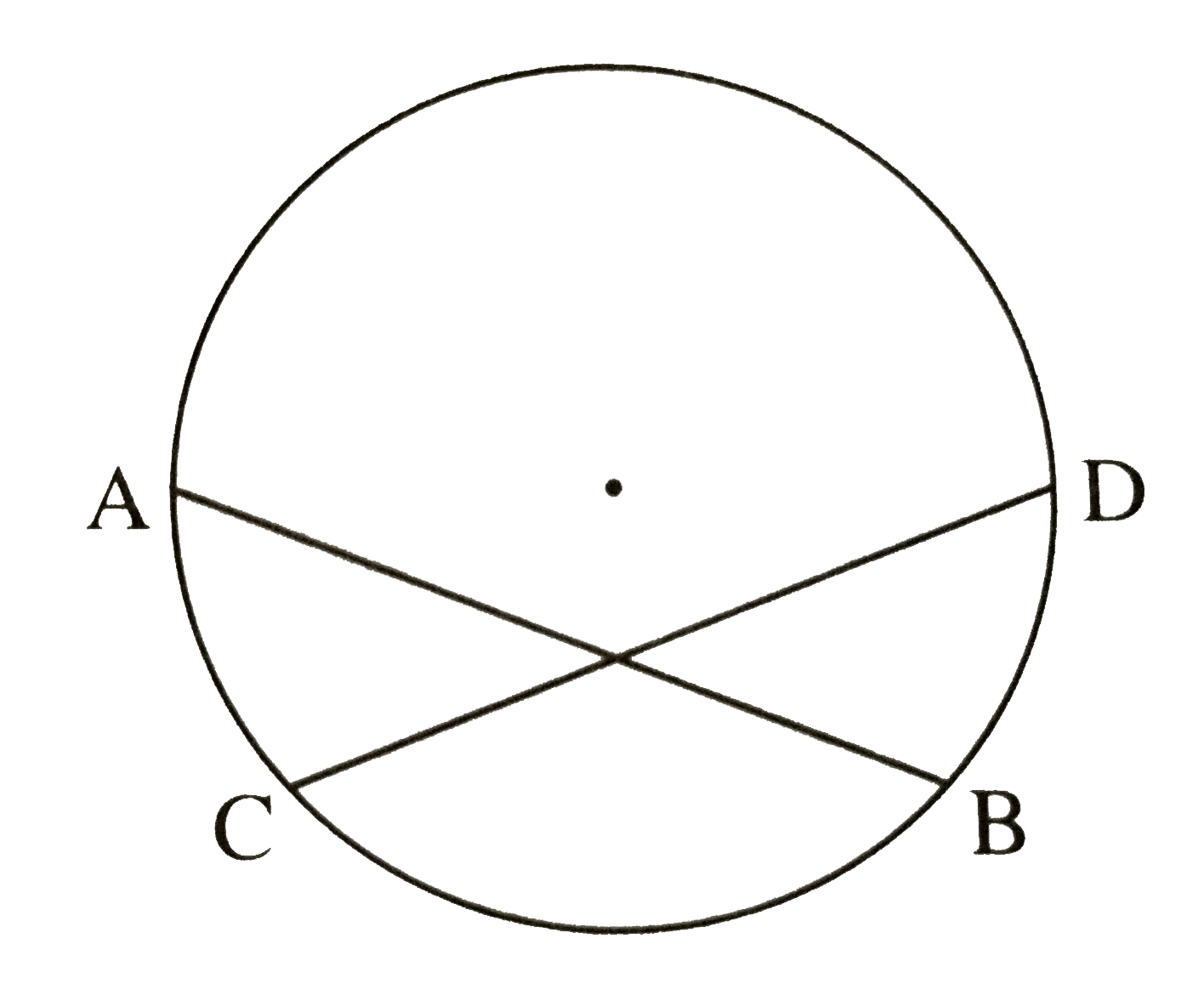
View SolutionIn figure, chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD.
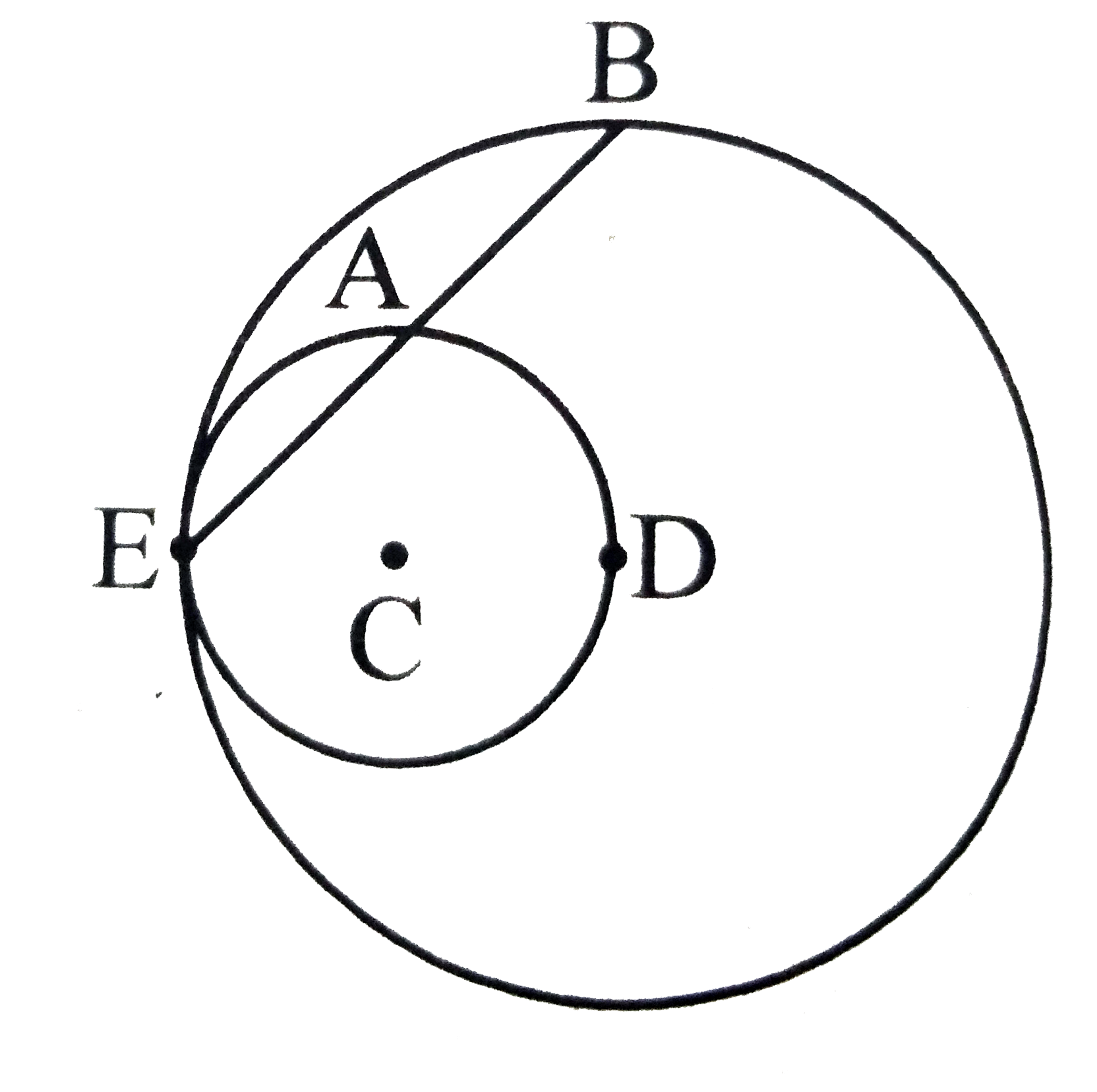
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
View Solution