A particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
r=Qq16π2ε0MT3
r3=Qq16π2ε0MT2
r2=Qq16π3ε0mT3
r2=Qq16π3ε0mT3
The correct Answer is:2
Step by step video, text & image solution for A particle of charge -q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1
8 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 2
10 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level II(C.W)
27 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
Knowledge Check
A particle of charge 'q' and mass 'm' move in a circular orbit of radius 'r' with frequency 'v' the ratio of the magnetic moment to angular momentum is:
A2qvmBqv2mCq2mrDq2mA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
Aω and qBω,q and mCq and mDω and mA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
Aω:qBq:mCq:2mDω:m
A particle of charge q and mass m moves in a circular orbit or radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA positive charge Q is fixed at a point in space. There is another charge -q, which moves in a circular path of radius r around the given fixed charge . Assume that the electrostatic force between them is the only force acting on them. Calculate time period of revolution of charge .
View SolutionA particle of the charged q and massm moves in a circular orbit of radius r with angular speed ω . The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
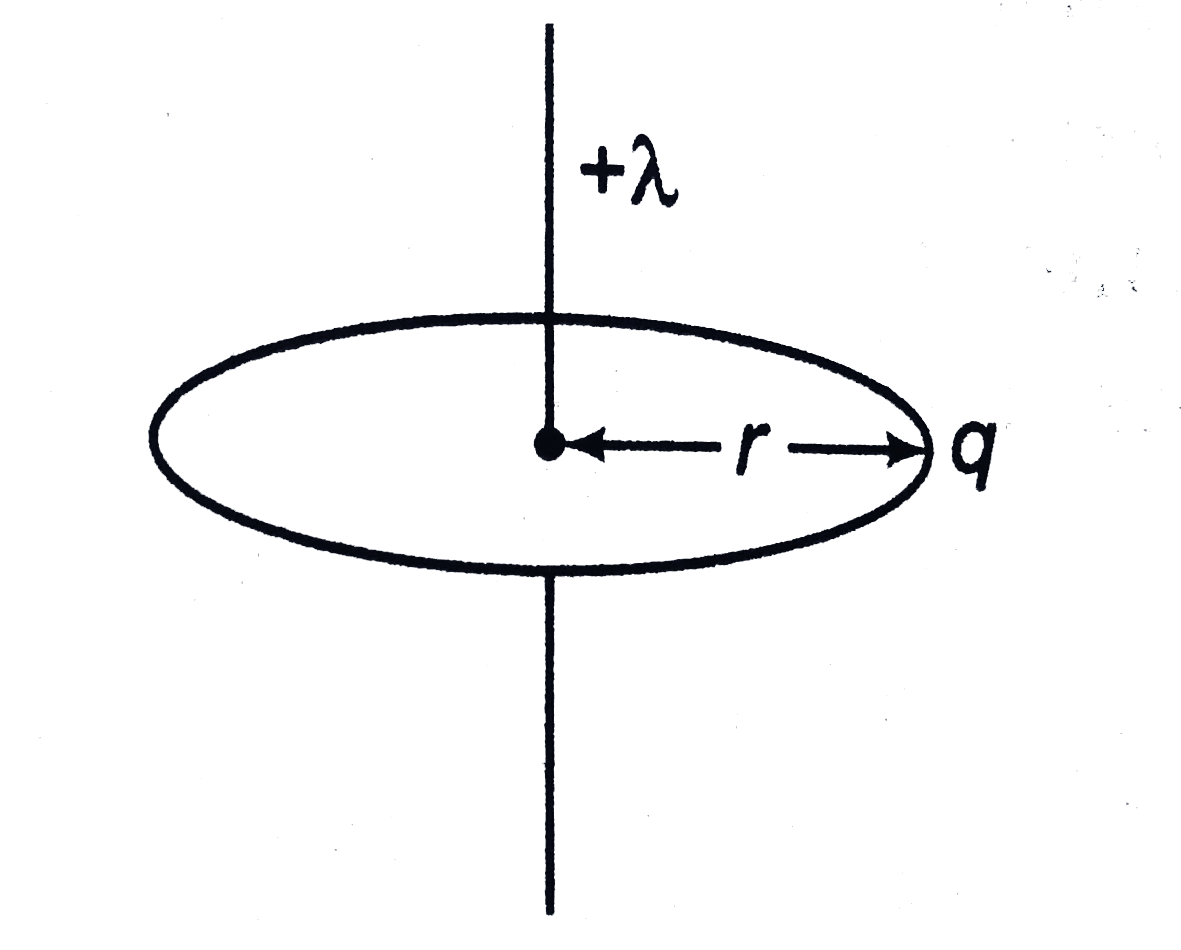 where , k=14πε0)
where , k=14πε0)
View SolutionWhen a charged particle of charge a revolves in a circular orbit of radius r with frequency n, then orbital current will be
View Solution
